2

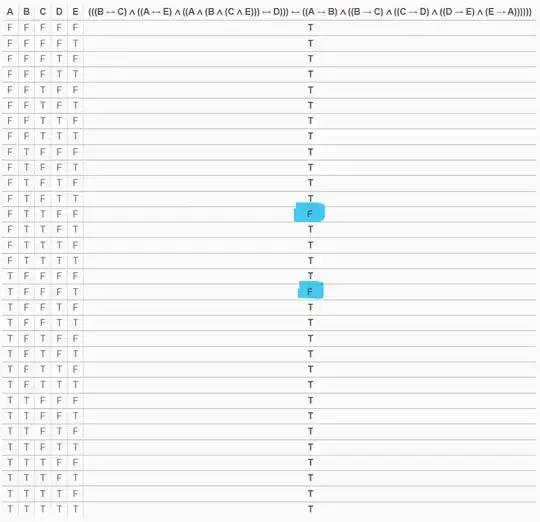
I want to prove that 5 statements are equivalent. I have been told that it is not necessary to prove $\binom{5}{2} = 20$ equivalences; we can show, for example, that $P_1 \implies P_2$, $P_2 \implies P_3$, $P_3 \implies P_4$, $P_4\implies P_5$ and $P_5 \implies P_1,$ "completing" the loop.

I've tried something different:

$$P_1 \iff P_5\\ P_2 \iff P_3\\P_1 \land P_2 \land P_3 \land P_5 \iff P_4$$

Is this also correct?

ryang
  • 38,879
  • 14
  • 81
  • 179
Uri Toti
  • 533
  • 2
    In the beginning, you perhaps want to write "... it is not necessary to prove ${5\choose 2}=20$ equivalences ..."? – Hagen von Eitzen Sep 14 '21 at 20:52
  • 1
    What do the commas mean in $P_1,P_2,P_3,P_5\Leftrightarrow P_5$? $(P_1\land P_2\land P_3\land P_5)\Leftrightarrow P_4$? $(P_1\lor P_2\lor P_3\lor P_5)\Leftrightarrow P_4$? $(P_1\Leftrightarrow P_4)\land (P_2\Leftrightarrow P_4)\land (P_3\Leftrightarrow P_4)\land (P_5\Leftrightarrow P_4)$? – Hagen von Eitzen Sep 14 '21 at 20:55
  • It means the first thing you said. – Uri Toti Sep 14 '21 at 20:57
  • Assume you want to prove the bidirection $P_4 ⟺ P_i (i=1,2,3,5)$ from your last statement with conjunctive normal form on the left, have you tried or struggled with any deductive proof for either direction? Or tried some counterexample if you think it's false? For example from right to left implication direction, it's easy to spot $P_4 \rightarrow P_i (i=1,2,3,5)$ immediately from your last equivalence. But the issue is you cannot derive $P_i (i=1,2,3,5) \rightarrow P_4$ since all the 4 $P_i$ may not be simultaneously true. Had they been all true, your intuition will work out. – cinch Sep 15 '21 at 02:23
  • Actually yesterday there was a question here in this site which can give you the exact hint you need to proceed formally expected by your intuition about their logical equivalence, assuming all your Pi(i=1,2,3,5) are true (already proven or given), and you need an extra equivalence to link $P_1$ with $P_2$ (or $P_3$) to finish your intended loop... – cinch Sep 15 '21 at 02:52
  • I suppose I have to ask you, why do you have any doubts. As long as you can travel from any $P_i$ to any other $P_j$ you are okay. However to prove you can travel from any $P_i$ to any other $P_j$ is usually assumed far to tedious to prove and is usually considered intuitively obvious. And loop is one way be any T-path with bridges or loops will do. Your last case-- all $P_{i\ne 4}$ bridge to $P_4$ making $P_4$ a Grand Central Station should be clearly such a closed path. Why do you have doubts whether it is enough? – fleablood Sep 15 '21 at 22:53
  • @DonThousand Are you reading the OP's proposal according to Hagen's third suggested interpretation? Because that's the only interpretation that's consistent with your claim. – ryang Sep 16 '21 at 07:49

2 Answers2

2

  1. The lack of symmetry in your proposal

    • $P_1 \iff P_5$
    • $P_2 \iff P_3$
    • $P_1\land P_2\land P_3\land P_5 \iff P_4$

    suggests that they are not jointly equivalent to the original

    • $P_1 \implies P_2$
    • $P_2 \implies P_3$
    • $P_3 \implies P_4$
    • $P_4\implies P_5$
    • $P_5 \implies P_1.$

  2. Rob has given a counter-interpretation; here's another one $$P_1 :=\; 7=7\\ P_5 :=\; 7=7\\ P_2 :=\; 8=9\\ P_3 :=\; 8=9\\ P_4 :=\; 8=9,$$ and yet another one $$P_2 :=\; 7=7\\ P_3 :=\; 7=7\\ P_1 :=\; 8=9\\ P_4 :=\; 8=9\\ P_5 :=\; 8=9.$$ The $5$ (non-equivalent) statements in each interpretation jointly satisfies the first (your proposal)—but not the second (the original)—set of sentences.


  3. enter image description here

  4. Here's an example set of sentences that is jointly equivalent to the original set:

    • $P_1\implies P_2\land P_3\land P_4\land P_5$
    • $\lnot P_1\implies\lnot P_2\land \lnot P_3\land \lnot P_4\land \lnot P_5.$

    (Assume, without loss of generality, that $P_3$ is true; then, by contraposition, so is $P_1;$ consequently, so are the three remaining statements.)

    Another that works is Hagen's last suggestion in their second comment under the OP.

ryang
  • 38,879
  • 14
  • 81
  • 179
0

Assume that $x$ ranges over the integers. Take $P_1$ and $P_5$ both to be $x \ge 0$. Take $P_2$ and $P_3$ both to be $x \le 1$. Finally take $P_4$ to be $x \ge 0 \land x \le 1$. Then $P_1 \iff P_5$, $P_2 \iff P_3$ and $P_1 \land P_2 \land P_3 \land P_5 \iff P_4$ are all valid, but $P_4$ is, strictly stronger than, and hence not equivalent to, any of the other $P_i$. So given your answer to the comment about your notation, your proposal is not a valid way to prove the equivalence of the $P_i$.

Rob Arthan
  • 48,577
  • I agree your constructed P4 statement is stronger in the sense of location targeting on the real line, but this is not the criterion for logical equivalence between statements. I think the real missing link for PO to complete the loop is an extra logical equivalent of P1 and P2, they may not be logically equivalent at all as shown in your example. Also I'm not convinced the implication direction from left 4 conjuncts to right side of P4 since left side is a closed interval [0,1] while P4 locates x only at either end of this interval, so here you derived a "stronger" result, can you elaborate? – cinch Sep 15 '21 at 05:18
  • 1
    @mohottnad: thanks for drawing my attention to a mistake in my definition of $P_4$. I have fixed that. As for you first point, to prove that a proposed method of proof, comprising some hyptotheses and a conclusion, is invalid, what you need to do is produce an example that satisfies the hyptotheses but not the conclusion. That is exactly what I have done here. – Rob Arthan Sep 15 '21 at 19:40