0

I want to solve $$\iiint_E 1\,dx\,dy\,dz$$ for $E=\{(x,y,z)\mid |x|+|y|+|z|\leq 1\}$.

My attempt:

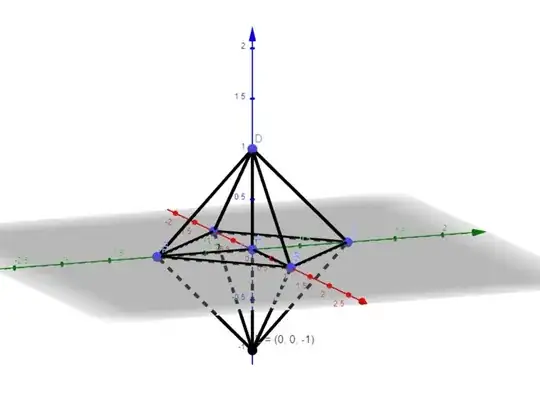
I thought about it graphically. The region is like having a tetrahedron for each octant of the coordinate-system, right? Then we would have a shape like this:

enter image description here

So I'd say that the integral should be $0$ because of symmetry.

But I'd like to calculate it explicitely. This is how I came up for the tetrahedron at $(0,0,0),(1,0,0),(0,1,0),(0,0,1)$: \begin{align*} \int_0^1 \int_0^{1-z} \int_0^{1-y-z} 1 \,dx\, dy \,dz = 1/6 \end{align*}

But I don't know how I should change the bounds to calculate the tetrahedrons of the other areas. They should result in either $-1/6$ or $1/6$.

I'd like to have some help with that.

Jochen
  • 2,260
Quotenbanane
  • 1,594
  • 2
    The region is symmetric, but the integrand is identically $1$ so that the integral is the volume of a solid. Its volume in the first octant is $1/6$, and the solid is symmetric in $x$, $y$, and $z$, so the volume is $1/6$ in each of the 8 octants. The total volume is $4/3$. – Umberto P. Jan 11 '22 at 18:18
  • 2
    Hello :) it can't be zero or less than zero because you integrate a positive-valued function. Further, if you integrate the one-function over a body, you get the volume of the body. Here it's a octahedron $E$, which can be decomposed to eight tetrahedrons of volume $\frac 16$. Hence, we get $\frac 86$ as desired value. – Jochen Jan 11 '22 at 18:21
  • @Jochen Yes, that's true. I was too much thinking about school where you get negative and positive values out of the integration but here I want to calculate the total area. So yes it's $8\cdot \frac{1}{6}$. Thanks Jochen & Umberto. – Quotenbanane Jan 11 '22 at 18:24
  • https://math.stackexchange.com/q/3063441/321264 – StubbornAtom Jan 11 '22 at 18:35
  • Does this answer your question? What is the volume of the region $S ={(x, y, z) : |x| + |y| + |z| ≤ 1}$? – Anne Bauval Jun 14 '23 at 08:27

1 Answers1

1

I would write the integration of the entire region, before I split into tetrahedrons. If you start with $z$, you need to integrate between $-1$ and $1$. Then based on your condition $y$ varies between $-(1-|z|)=|z|-1$ and $1-|z|$. Similarly, $x$ varies between $-(1-|z|-|y|)=|y|+|z|-1$ and $1-|z|-|y|$. Now depending on the sign, you have two regions for $x$, two for $y$ and two for $z$, total $2\cdot2\cdot2=8$ regions.

Let's choose any region, say positive $z$, negative $y$ and positive $x$. Then the smallest positive $x$ is $0$, the maximum is $1-|z|-|y|$. Since $z$ is positive and $y$ is negative, you have $$1-|z|-|y|=1-z+y$$ Then for the $y$ integration, the maximum value is $0$ and the minimum is $-(1-|z|)=z-1$. Therefore $$V_{+-+}=\int_0^1\int_{z-1}^0\int_0^{1-z+y}dxdydz$$ Following a similar reasoning, you should be able to find all the limits. Let me know if you need another example.

Andrei
  • 37,370