show that
$$\int_{0}^{\infty } \frac{\sin (ax)}{x(x^2+b^2)^2}dx=\frac{\pi}{2b^4}\left(1-\frac{e^{-ab}(ab+2)}{2}\right)$$
for $a,b> 0$
I would like someone solve it using contour but also I would to see different solution using different way to solve it
is there any help thanks for all
$$\int_0^{\infty} \frac{\sin ax\,dx}{x(x^2+b^2)^2}=\frac{1}{b^4}\left(\int_0^{\infty}\frac{\sin ax}{x}\,dx-\int_0^{\infty}\frac{x\sin ax\,dx}{x^2+b^2}\right)-\frac{1}{b^2}\int_0^{\infty}\frac{x\sin ax\,dx}{(x^2+b^2)^2}$$
The first integral is well known. For any $a>0:$
$$\int_0^{\infty} \frac{\sin ax}{x}\,dx=\frac{\pi}{2}$$
The second, consider:
$$\begin{aligned}f(t)=\int_0^{ \infty} \frac{x\sin axt\,dx}{x^2+b^2}\,dx \Rightarrow \mathcal{L} \{ f(t)\} &=\int_0^{ \infty}e^{-st}\int_0^{ \infty}\frac{x\sin axt\,dx}{x^2+ b^2}\,dx\,dt\\&=\int_0^{ \infty}\frac{x}{x^2+ b^2}\int_0^{\infty}e^{-st}\sin axt\,dt\,dx\\&=\int_0^{\infty} \frac{ax^2}{(x^2+ b^2)(a^2x^2+s^2)} \,dx\\&= \frac{\pi}{2(s+ab)}\end{aligned}$$
$$\frac{\pi}{2}\cdot\mathcal{L}^{-1}\left\{ \frac{1}{s+ab}\right\}\Bigg|_{t=1}= \frac{\pi}{2e^{ab}}$$
The third, using the same parameter (call the function $g(t)$ now) one obtains:
$$\begin{aligned}\mathcal{L} \{ g(t)\} &=\int_0^{ \infty}\frac{x}{(x^2+ b^2)^2}\int_0^{\infty}e^{-st}\sin axt\,dt\,dx\\&=\int_0^{\infty} \frac{ax^2}{(x^2+ b^2)^2(a^2x^2+s^2)} \,dx\\&= \frac{a\pi}{4b(s+ab)^2}\end{aligned}$$
$$\frac{\pi a}{4b}\cdot\mathcal{L}^{-1}\left\{ \frac{1}{(s+ab)^2}\right\}\Bigg|_{t=1}= \frac{a\pi}{4be^{ab}}$$
Therefore:
$$\int_0^{\infty} \frac{\sin ax\,dx}{x(x^2+b^2)^2}=\frac{\pi}{2b^4}\left(1-\frac{2+ab}{2e^{ab}}\right)$$
You can consider employing the residue theorem. The trick is to use a simple contour despite the pole at $z=0$. A way to attack this is to deform the usual semicircular contour at the origin so as not to include the pole.
Consider first the case $a>0$. Rewrite the integral as
$$\frac12 \int_{-\infty}^{\infty} dx \frac{\sin{a x}}{x (x^2+b^2)^2} = \frac{1}{4 i} \int_{-\infty}^{\infty} dx \frac{e^{i a x} - e^{-i a x}}{x (x^2+b^2)^2}$$
Therefore consider the contour integral
$$\frac{1}{4 i} \oint_C dz \frac{e^{i a z}}{z (z^2+b^2)^2}$$
where $C$ is as described above, a semicircle of radius $R$ in the upper half plane, with a semicircle of radius $\epsilon$ about the origin jutting into the upper half plane. Note then that the pole at the origin is not within $C$.
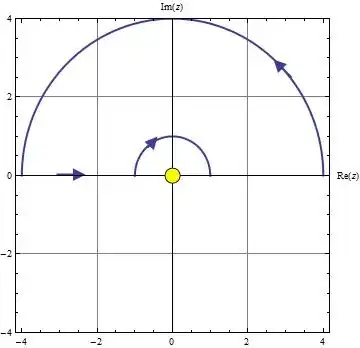
Then the above contour integral is equal to
$$\frac{1}{4 i} \int_{-R}^{-\epsilon} dx \frac{e^{i a x}}{x (x^2+b^2)^2} + \frac{\epsilon}{4} \int_{\pi}^0 d\phi \, e^{i \phi} \frac{e^{i a \epsilon e^{i \phi}}}{\epsilon e^{i \phi} (\epsilon^2 e^{i 2 \phi}+b^2)^2} + \frac{1}{4 i} \int_{\epsilon}^{R} dx \frac{e^{i a x}}{x (x^2+b^2)^2} + \\ \frac{R}{4} \int_0^{\pi} d\theta\, e^{i \theta} \frac{e^{i a R e^{i \theta}}}{R e^{i \theta} (R^2 e^{i 2 \theta}+b^2)^2} $$
We take the limit as $R \to \infty$ and $\epsilon \to 0$ and the contour integral then becomes
$$\frac{1}{4 i} PV \int_{-\infty}^{\infty} dx \frac{e^{i a x}}{x (x^2+b^2)^2} -\frac{\pi}{4 b^4} $$
where $PV$ denotes the Cauchy principal value. Note that the fourth integral vanishes as
$$\frac{1}{R^4} \int_0^{\pi} d\theta \, e^{-a R \sin{\theta}} \le \frac{2}{R^4} \int_0^{\pi/2} d\theta \, e^{-2 a R \theta/\pi} = \frac{\pi}{R^5}\frac{1-e^{-a R}}{a} $$
The contour integral is also equal to $(1/(4 i)) i 2 \pi$ times the residue of the integrand at the pole $z=i b$. Because we have a double pole, the residue has value
$$\begin{align}\frac{d}{dz} \left [ \frac{e^{i a z}}{z (z+i b)^2}\right ]_{z=i b} &= -\left (\frac{a b+2}{4 b^4} \right ) e^{-a b}\end{align}$$
Therefore
$$\frac{1}{4 i} PV \int_{-\infty}^{\infty} dx \frac{e^{i a x}}{x (x^2+b^2)^2} = \frac{\pi}{4 b^4} \left [1-\frac12 (2+a b) e^{-a b} \right ]$$
when $a>0$. Similarly, one may find that, for $a>0$:
$$\frac{1}{4 i} PV \int_{-\infty}^{\infty} dx \frac{e^{-i a x}}{x (x^2+b^2)^2} = -\frac{\pi}{4 b^4} \left [1-\frac12 (2+a b) e^{-a b} \right ]$$
(Note that the contour integral in this case is $(1/(4 i) (-i 2 \pi)$ times the residue at $z=-i b$ because the contour in the lower half plane is taken clockwise rather than counterclockwise.) Therefore, for $a>0$,
$$\int_0^{\infty} dx \frac{\sin{a x}}{x (x^2+b^2)^2} = \frac{\pi}{2 b^4} \left [1-\frac12 (2+a b) e^{-a b} \right ]$$
I would start with the known result (from this site!) Link
$$\int_{0}^{\infty } \frac{\cos (tx)}{x^2+b^2}dx=\frac{\pi}{2}\frac{e^{-tb}}{b}$$
Now, all you need is integrate the result with respect to $t$ from $t=0$ to $t=a$ and differentiate it with respect to $b$
$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ $\ds{\bbox[5px,#ffd]{}}$
Here is a related hint. First, note that
$$ \int_{0}^{\infty } \frac{\sin (ax)}{x(x^2+b^2)^2}dx=\frac{1}{2}\int_{-\infty}^{\infty } \frac{\sin (ax)}{x(x^2+b^2)^2}dx .$$
Now, you can consider the complex integral
$$ \int_{C} \frac{e^{iaz}}{z(z^2+b^2)^2}dz.$$
