1

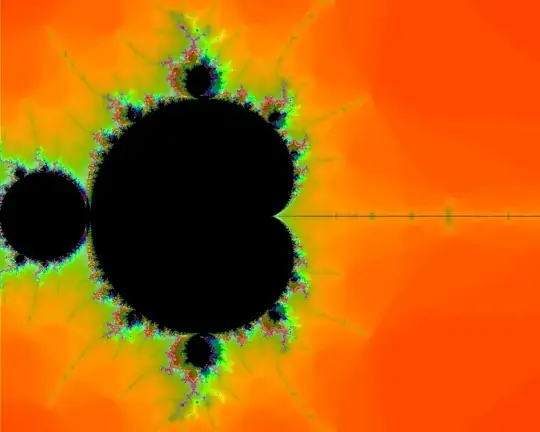
Although not all of the mini Mandelbrots exact copies of the whole set (for example, look at this question), are the mini Mandelbrots on the X-axis exact copies of the whole set?

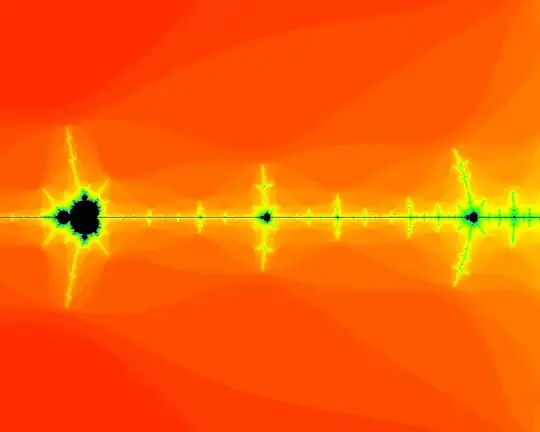
Here are some examples of them

More specifically, if we shrink the entire Mandelbrot set and move it to the location of any of these mini Mandelbrots, will it perfectly overlap onto them? (Obviously not in a trivial way like shrinking it almost completely and then putting it inside the cardioid of one of them...)

If so, is there any proof for this?

Thanks!

John Alexiou
  • 13,816
Peleg Michael
  • 41
  • 2
    No, they are not exact copies. – GEdgar Oct 26 '22 at 23:22
  • @GEdgar I tried to confirm on some and you're correct, thanks! – Peleg Michael Oct 26 '22 at 23:48
  • No mini Mandelbrot within the Mandelbrot set is an exact copy of the whole Mandelbrot set, because there is only one perfect circle in the whole Mandelbrot set. See https://math.stackexchange.com/questions/1857237/perfect-circles-in-the-mandelbrot-set – Claude Oct 27 '22 at 13:39

2 Answers2

2

As pointed out, they are not exact copies.

For example, here is an overlay of two parts, and clearly they don't perfectly overlap:

311411
  • 3,537
  • 9
  • 19
  • 36
Peleg Michael
  • 41
1

According to the journal article here, the period $3$ hyperbolic components are given by

$$c=-\frac{7}{4}-\frac{20}{9} \left[ \sinh \left( \omega (z)+\frac{2k\pi i}{3} \right)-\frac{1}{4\sqrt{5}} \right]^2$$

$$\omega (z)=\frac{1}{3}{\operatorname {Arcsinh}} \left( \frac{88 - 27z}{80\sqrt{5}} \right)$$

Expanding numerically into Fourier series in $z=e^{i\theta}$ for $k=0$:

$$c=-1.754877666+0.009517759z(1-0.461468994z-0.026854399z^2+\ldots)$$

which is not a perfect cardioid.

Compare with the hyperbolic components for periods $1$ and $2$ here.

Ng Chung Tak
  • 18,990