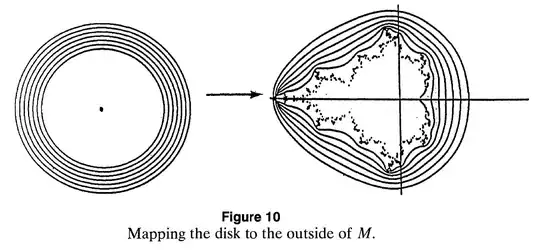
Apologies if this question has been asked here before. The Mandelbrot set is the set of complex numbers $c$ for which the iteration $z_{n+1}(c)=z_n (c)^2+c$ with $z_0(c)=0$ does not diverge (we write $z_\infty(c)=\lim\limits_{n\rightarrow\infty}z_n(c)$ where it converges). Thus every $z_n(c)$ can be written as a polynomial in $c$ of order $2^{n-1}$, so we define:
$$z_n(c)=\sum_{j=0}^\infty \beta_{n,j}c^j$$
where $\beta_{n.j}$ is only nonzero for $j\le2^{n-1}$. Using the Mandelbrot iteration formula and the Cauchy product, we get:
$$\beta_{n+1,j}=\begin{cases}\sum\limits_{k=0}^j\beta_{n,k}\beta_{n,j-k}&j\ne1\\2\beta_{n,0}\beta_{n,1}+1&j=1\end{cases}\tag{1}$$
Now $\beta_{n,0}=0\;\;\forall n\ge0$ and $\beta_{n,1}=1\;\;\forall n\ge1$ and using $(1)$ we can show that $\beta_{n+1,2}=\beta_{n,1}^2=1\;\;\forall n\ge1$, that $\beta_{n+1,3}=2\;\;\forall n\ge2$ and in general that $\beta_{n,j}=\beta_j\;\;\forall n\ge j$ where:
$$\beta_j=\begin{cases}0&j=0\\1&j=1\\\sum\limits_{k=0}^j \beta_k\beta_{j-k}&j\ge2\end{cases}$$
(I calculated the first few terms $0,1,1,2,5,14,42,132,429,...$ by hand, but the OEIS would not give me a general formula). Thus the first $n+1$ terms of $z_n(c)$ are $\beta_i c^i$ as seen here in red:
$$z_0(c)=\color{#ff0000}{0}$$ $$z_1(c)=\color{#ff0000}{0+c}$$ $$z_2(c)=\color{#ff0000}{0+c+c^2}$$ $$z_3(c)=\color{#ff0000}{0+c+c^2+2c^3}+\color{#0000ff}{c^4}$$ $$z_4(c)=\color{#ff0000}{0+c+c^2+2c^3+5c^4}+\color{#0000ff}{6c^5+6c^6+4c^7+c^8}$$
and so on. Thus as $n\rightarrow\infty$ the first $n+1$ terms of $z_n(c)$ will tend to the following series:
$$z(c)=\sum_{j=0}^\infty\beta_j c^j\tag{2}$$
However, because of the extra $2^{n-1}-n$ terms in $z_n(c)$ (shown in blue), I assume that $\{z_n(c)\}$ will not always converge to $z(c)$, especially since the Mandelbrot set is not a disc (and power series converge within discs), but I do not know of any way of describing the extra terms which will enable a connection to be made between the convergence of the Mandelbrot iteration and the convergence of $(2)$.
My questions are the following:
- For what $c$ are $\color{blue}{the\ blue\ terms}$ small enough that $z(c)=z_\infty(c)$,
- How if at all is the convergence of $(2)$ connected with the convergence of the iteration $z_{n+1}=z_n^2+c$?
- I would also to like to know whether there is a closed form for $z(c)$ [see comment]
- What is the radius of convergence of $(2)$?