This is Exercise 12.12 in the Ross textbook

and I found the solution like the below, but I'm not sure how the yellow line is resulted from the above lines. Can you help me understand this solution please?
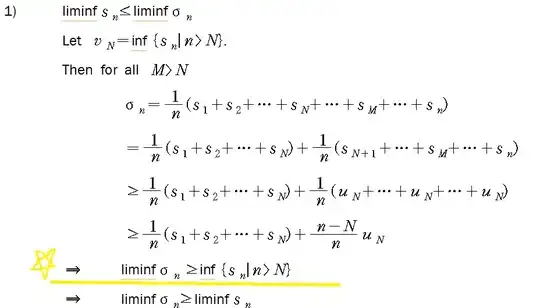
This is Exercise 12.12 in the Ross textbook

and I found the solution like the below, but I'm not sure how the yellow line is resulted from the above lines. Can you help me understand this solution please?
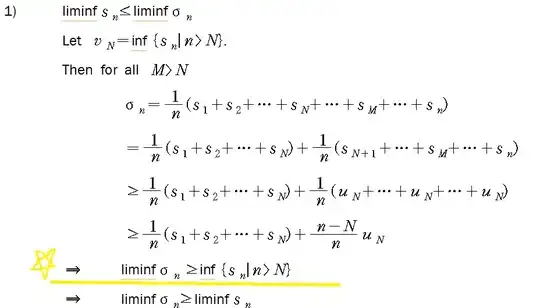
That is why it is always better to include more words. Consider the sequence defined by $v_n=\inf\{s_k:k>n\}$. Note that $\lim\limits_{n\to\infty}v_n=\liminf\limits_{n\to\infty}s_n$. Now, fix $N>0$, then take $M>N$. Whenever $n>M$ we will have that
$$\begin{align}\sigma_n&=\frac 1 n\left(s_1+\cdots+s_N+s_{N+1}\cdots+s_M+\cdots+s_n\right)\\&=\frac{1}{n}(s_1+\cdots+s_N)+\frac 1 n(s_{N+1}+\cdots+s_{M}+\cdots s_n)\\&\geq\frac{1}{n}(s_1+\cdots+s_N)+\frac{1}{n}(v_N+\cdots+v_N+\cdots +v_N)\\&=\frac 1 n(s_1+\cdots+s_N)+\frac{N-n}{n}v_N\end{align}$$
Since $N$ is fixed we will have, by taking $\liminf\limits_{n\to\infty}$ that $$\liminf\limits_{n\to\infty}\sigma_n\geq v_N$$ for each $N>0$. This means $$\liminf\limits_{n\to\infty}\sigma_n\geq \liminf_{n\to\infty }s_n=\lim_{N\to\infty }v_N$$