If $\sigma_n=\frac{s_1+s_2+\cdots+s_n}{n}$ then $\operatorname{{lim sup}}\sigma_n \leq \operatorname{lim sup} s_n$

Question

This is a question from the book Methods of Real Analysis by R. R. Goldberg.

If $(s_n)$ is a sequence of real numbers and if $$\sigma_n=\frac{s_1+s_2+\cdots+s_n}{n}$$ then prove that: $\operatorname{{lim sup}}\sigma_n \leq \operatorname{lim sup} s_n$.

I don't have any idea how to start working on this problem. Please help. Thanks.

Answer 1

Fix an integer $k$. Let $n\geqslant k$. Then $$\sigma_n=\frac 1n\sum_{j=1}^ks_j+\frac 1n\sum_{j=k+1}^ns_j\leqslant \frac 1n\sum_{j=1}^ks_j+\frac{n-k}n\sup_{l\geqslant k}s_l.$$ Now take on both sides the limsup when $\color{red}{n\to +\infty}$: we get the wanted result.

Taking $s_n:=(-1)^n$, we can see that the inequality may not be an equality.

Answer 2

[I've been working through Goldberg myself and found this question looking for an explanation myself. I think I eventually figured it out.]

Since this is from Goldberg, I'll point out that the problem statement suggests using his Theorem 2.9L, which essentially uses the interpretation in this Wikipedia article as an alternate definition of $\limsup$ and $\liminf$:

1. $\limsup_{n\to \infty} s_n = M$ means for any $\epsilon > 0$, (a) $s_n < M + \epsilon$ for all but a finite number of values of $n$; (b) $s_n > M - \epsilon$ for infinitely many values of $n$
2. (omitted similar def. for $\liminf$).

(He mentions it's an if and only if relationship, while only proving the "if" direction.)

If you peek ahead a bit to 2.11B, Goldberg happens to prove some things about Cesàro summability $(C,1)$, and you get very close to the desired proof because he uses the same technique he hinted at in this problem.

For the particular problem, by his alternate definition, for some $N_0$, $s_n < M + \epsilon$ if $n > N_0$ (and similarly, for some $N_1$, all $s_n < M + \frac{\epsilon}{2}$ if $n > N_1$).

Can we get $\sigma_n$ to eventually fit below $M + \epsilon$ too?

Proceeding as in the accepted answer and splitting the sum into two, the ultimately goal becomes finding a large enough $N_2$ such that $\sigma_n$ (which equals the sum of those two sums) is also smaller than $M + \epsilon$ (for arbitrary $\epsilon$ and all $n > N_2$).

An image may help motivate this:

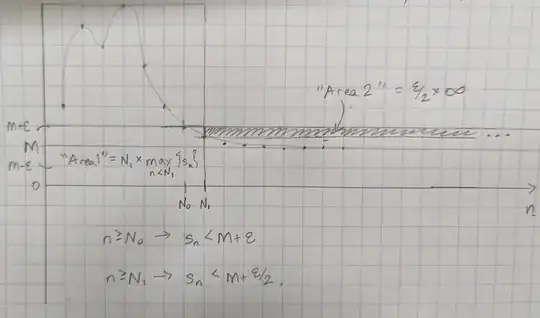
The intuition is to "leave some room" between $M + \frac{\epsilon}{2}$ and $M + \epsilon$ such that the sum of the portions for the lower-indexed $s_i$ in $\sigma_n$ can be balanced out in some portion of the $\frac{\epsilon}{2}$-high strip extending from $N_1$ out to infinity.

(Here I'm thinking of the discrete sums as analogous to areas: can the area before $N_1$ fit into the area between $M+\frac{\epsilon}{2}$ and $M+\epsilon$? The answer seems pretty clearly yes to me based on the picture, but I still have to demonstrate the existence of some $N_2$ that works.)

The following reasoning seems to work (at least if $M \ge 0$, which can probably be made more rigorous for by translating each term of the sequence up by a well chosen constant and then undoing that later):

\begin{align} \sigma_n &= \frac{1}{n}\sum_{i=1}^{N_1}s_i + \frac{1}{n}\sum_{i=N_1+1}^n s_i \\\\ &\le \frac{N_1}{n}\max_{1\le i\le N_1}|s_i| + \frac{n-N_1}{n}(M + \frac{\epsilon}{2}) \\\\ &= M + \frac{\epsilon}{2} - \frac{N_1}{n}(M + \frac{\epsilon}{2}) + \frac{N_1}{n}\max_{1\le i\le N_1}|s_i| \end{align}

Doing some messy math we want to get the sum of the last two terms to be less than $\frac{\epsilon}{2}$ so that the whole $\sigma_n \le M + \epsilon$ (and therefore $\limsup_{n\to \infty} \sigma_n \le M$). Any $n \ge N_2 = \lceil\frac{2N_1}{\epsilon}(\max_{1\le i\le N_1}|s_i| - M - \frac{\epsilon}{2})\rceil$ seems to fit the bill.

Answer 3

Here's a simple solution:

Let $x^{*}_k = \sup_{k \geq n} \{x_n\}$. Then, $$x^{*}_k \to \limsup_{n \to \infty} \{x_n\}.$$

By a simple fact, a convergent sequence's averages converge to the same limit, so $$\sigma_n^{*} = \frac{1}{n} \sum_{j=1}^{n} x^{*}_j \to \limsup_{n \to \infty} \{x_n\}$$ as well. Now since $\sigma_n \leq \sigma^{*}_n$, the result follows.