Angle of tilt of a cup so that the water surface touches the rim

Question

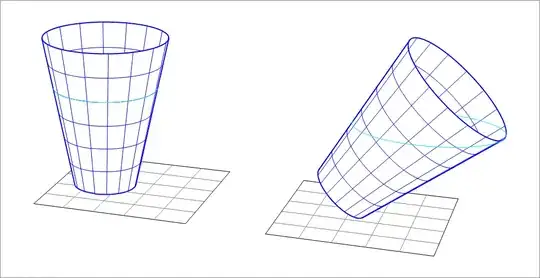
A cup is in the shape of a right circular conical frustum with bottom diameter $4 cm$ and top diameter $8 cm$, and slant height $10 cm$. It is filled to $\dfrac{2}{3}$ of its height with water, then the cup is tilted by an angle $\theta$ such that the water surface touches the rim of the cup (See attached image). Find the tilt angle $\theta$.

My attempt:

First, complete the frustum down to the vertex of the cone. Compute the volume of the cone from the vertex to the water surface, let this volume be $V_0$. Next, I derived that the ellipse of the cut has a semi-major axis length $a$ and semi-minor axis length $b$ where,

$ a = \dfrac{ z_0 \tan \theta_c \cos \theta }{ 1 - \sin^2 \theta \sec^2 \theta_c } $

$ b = \dfrac{ z_0 \tan \theta_c \cos \theta }{ \sqrt{1 - \sin^2 \theta \sec^2 \theta_c} } $

where $\theta_c$ is the semi-vertical angle of the cone (i.e. the angle between the axis of the cone and its surface). $z_0$ is the distance between the vertex and the intersection point of the axis with the cutting plane. $\theta$ is the acute angle between the axis of the cone and the normal vector to the cutting plane.

In addition, the altitude of the tilted cone (the perpendicular distance between the vertex of the cone and the cutting plane) can be computed as $z_0 \cos \theta $. Also, $z_0$ can be directly related to the slant height (along the side of the cup) and angles $\theta_c$ and $\theta$.

With all that, the volume of water in the tilted cup can be expressed as function of $\theta$ and equated to $V_0$ (the volume before tilting). The resulting equation can be simplified into a simple trigonometric equation in double the angle $\theta$, and can be solve for $\theta$. With the given values, I found that the tilt angle $ \theta = 41.458^\circ $

Any comments, hints, and alternative solutions are highly appreciated.

Answer 1

Hint.

Let us consider a cone instead of a truncated cone. The cone equation is given by

$$ C_{\lambda}(x,y,z) = x^2+y^2-\lambda^2z^2=0 $$

now rotating $\vec n = (0,0,1)$ around de axis $(0,1,0)$ by an angle $\theta$ we obtain $\vec n_{\theta} = (\sin\theta,0,\cos\theta)'$. After a tilt $\theta$ the liquid level can be described by the plane $P_{\theta}=\vec n_{\theta}\cdot(p-p_0)=0$ where $p = (x,y,z)'$ and $p_0 = (x_0,0,x_0/\lambda)'$. Now solving $\vec n_{\theta}\cdot(p-p_0)=0$ for $z$ we obtain $z = (\lambda+\tan\theta)x_0-x\tan\theta$ and the tilted cone volume is given by

$$ V_{\theta}=\int_{\Omega(x,y,\theta)}\left((\lambda+\tan\theta)x_0-x\tan\theta-\frac{1}{\lambda}\sqrt{x^2+y^2}\right)d\Omega $$

Here

$$\Omega(x,y,\theta) = C_{\lambda}(x,y,z)\cap P_{\theta}=\cos ^2\theta \left(\lambda ^4 x_0^2-x^2-y^2\right)-\lambda ^2 (x-x_0) \sin \theta(2 \lambda x_0 \cos\theta+(x_0-x)\sin\theta ) \ge 0$$

Finally we can obtain the tilt angle by solving for $\theta$

$$ V_0 = \frac 13\frac{\pi}{\lambda} x_0^3=V_{\theta} $$

Answer 2

Let $r_1$ be the bottom radius, and $r_2$ be the top radius, and $h$ be the height of the frustum.

Also let $\theta_c$ be the semi-vertical angle of the cone. Then the slant height $h_S$ and the height $h$ are related by $ h_S^2 = h^2 + (r_2 - r_1)^2 $

Assuming the cup is resting on the $xy$ plane with its base centered at the origin, complete the cone frustum down to the vertex of the cone. The base be at $z = 0$ and the top is at $z = h$. The radius r is related to the altitude $z$ by the linear relation

$r = r_1 + (z / h) (r_2 - r_1)$

so, for example, the radius of the water surface is $ r_3 = r_1 + (w / h) (r_2 - r_1) $ where in this problem $w/h = \dfrac{2}{3} $.

Then when $r = 0$ (the vertex of the cone), we have

$ Z_V = h (-r_1 ) / (r_2 - r_1) $

Note that $Z_V$ is negative.

The height of the cone from the vertex to the water surface is

$ Z_{Top} = - Z_V + w = (w + h r_1 / (r_2 - r_1) ) $

So, the volume of the cone from the vertex up to the water surface is

$V_1 = 1/3 \pi r_3^2 Z_{Top}$

Now we'll tilt the cone about the vertex by an angle $\theta$.

The water surface will intercept the axis of the cone at z_0 (unknown) away from the vertex.

The slant height of the cone is given by

$s = (h - Z_V) \sec \theta_c$

And from equality of vertical height above the vertex, we get

$ s \cos( \theta + \theta_c ) = z_0 \cos \theta $

so that

$ z_0 = s \dfrac{ \cos( \theta + \theta_c ) }{ \cos \theta } $

The altitude of the tilted cone from the vertex to the water surface is given by $ z_0 \cos \theta $

The ellipse of the water surface has a semi-major axis given by

$ a = \dfrac{z0 \tan \theta_c \cos \theta }{ 1 - \sin^2 \theta \sec^2 \theta_c } $

and a semi-minor axis length

$ b = \dfrac{z0 \tan \theta_c \cos \theta }{ \sqrt{1 - \sin^2 \theta \sec^2 \theta_c} } $

Hence the equation we want to solve for $\theta$ is

$ (1/3) \ \pi \ r_3^2 \ Z_{Top} = (1/3) \ \pi \ \dfrac{ z_0^3 \tan^2 \theta_c \cos^3 \theta }{(1 - \sin^2 \theta \sec^2 \theta_c)^{3/2} }$

Simplifying, and raising both sides to the power $(2/3) $, gives us,

$ K = \dfrac{ z_0^2 \cos^2 \theta }{ 1- \sin^2 \theta \sec^2 \theta_c } $

where

$K = \dfrac{r_3^{4/3} Z_{Top}^{2/3} }{ (\tan \theta_c) ^{4/3} } $

Therefore,

$ K ( 1 - \sin^2 \theta \sec^2 \theta_c ) = z_0^2 \cos^2 \theta = ((h - Z_V) \sec \theta_c)^2 \cos^2 (\theta + \theta_c) $

Using $\sin^2 \phi = 1/2 (1 - \cos(2 \phi) )$ and $\cos^2 \phi = 1/2 (1 + \cos(2 \phi) ) $

We get

$ K (1 - 1/2 \sec^2 \theta_c (1 - \cos(2 \phi) ) ) = 1/2 (h - Z_V)^2 \sec^2 \theta_c (1 + \cos(2 \theta + 2 \theta_c ) )$

Divide both sides by $(1/2) \sec^2 \theta_c$

$ K (2 \cos^2 \theta_c - (1 - \cos(2 \phi) ) ) = (h - Z_V)^2 (1 + \cos(2 \theta) \cos(2 \theta_c) - \sin(2 \theta) \sin(2 \theta_c) ) $

which is of the form

$ A \cos(2 \theta) + B \sin(2 \theta) = C $

with

$ A = K - (h - Z_V)^2 \cos(2 \theta_c) $

$ B = (h - Z_V)^2 \sin(2 \theta_c) $

$ C = (h - Z_V)^2 - K \cos (2 \theta_c) $

This simple trigonometric equation is readily solvable. Taking the smaller of the two solutions gives us $\theta$.