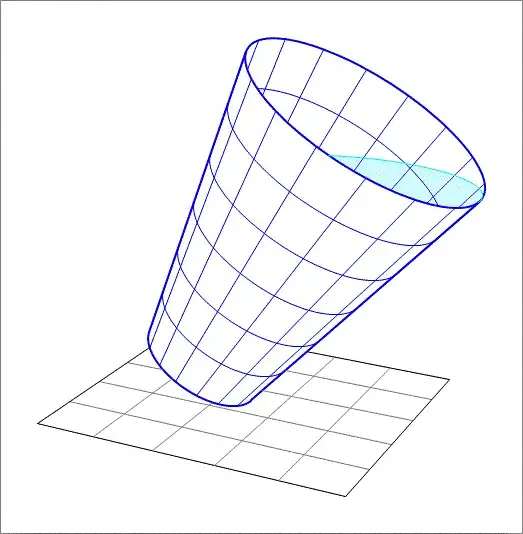
A cup takes the shape of a right circular conical frustum. The bottom radius is $r_1$ and the top radius is $r_2$ and its height is $h$. It is tilted from the vertical by an angle $\theta$. Find an expression of volume of water that will fill the cup to the rim.
My attempt:
By completing the cone to its vertex, we get the 'missing' altitude (the vertical distance between the vertex and the bottom of the cup). This distance is given by
$ Z_V = \dfrac{h r_1}{r_2 - r_1} $
Let the surface of water intersect the axis of the cone at a distance $z_0$ from its vertex, then using a simple diagram, we have
$s = (h + Z_V) \sec \theta_c$
where $\theta_c$ is the semi-vertical angle of the cone, and is given by
$ \theta_c = \tan^{-1} \dfrac{r_2 - r_1}{h} $
And from equality of vertical height above the vertex, we get
$ s \cos( \theta + \theta_c ) = z_0 \cos \theta $
From which we can calculate $z_0$
One can show that the semi-major axis $a$ and semi-minor axis $b$ of the water surface are given by
$ a = \dfrac{z0 \tan \theta_c \cos \theta }{ 1 - \sin^2 \theta \sec^2 \theta_c } $
$ b = \dfrac{z0 \tan \theta_c \cos \theta }{ \sqrt{1 - \sin^2 \theta \sec^2 \theta_c} } $
Putting all this together, we find that the volume of the cone is given by
$V = (1/3) \ \pi \ \dfrac{ z_0^3 \tan^2 \theta_c \cos^3 \theta }{(1 - \sin^2 \theta \sec^2 \theta_c)^{3/2} } $
From this volume we have to subtract the volume of the small cone whose base is the base of the cup, and this is given by
$V_0 = (1/3) \pi r_1^2 Z_V = 1/3 \pi r_1^3 \cot(\theta_c)$
Therefore the answer to the question is that volume is given by
$ V_{Water} = V - V_0 = \dfrac{\pi}{3} \ \bigg(\dfrac{ z_0^3 \tan^2 \theta_c \cos^3 \theta }{(1 - \sin^2 \theta \sec^2 \theta_c)^{3/2} } - r_1^3 \cot (\theta_c) \bigg)$