In a triangle ABC, prove that cot(A/2)+cot(B/2)+cot(C/2) =cot(A/2)cot(B/2)cot(C/2)

Question

In a triangle ABC, prove that $\cot \left ( \frac{A}{2} \right )+\cot \left ( \frac{B}{2} \right )+\cot \left ( \frac{C}{2} \right )=\cot \left ( \frac{A}{2} \right )\times \cot \left ( \frac{B}{2} \right )\times \cot \left ( \frac{C}{2} \right )$. I tried all identities I know but I have no idea how to proceed.

Answer 1

Here is a proof that does not use trigonometry:

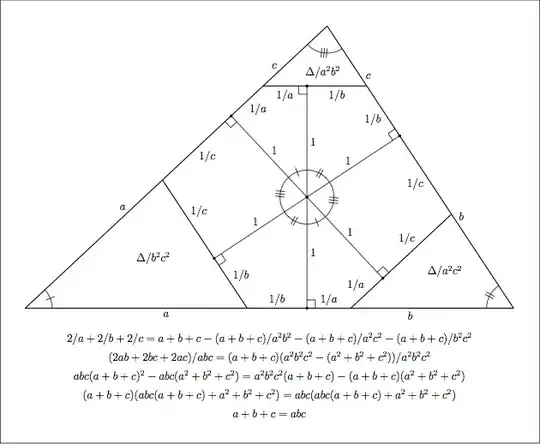
Source: my blog post.

Answer 2

HINT:

$$\frac A2+\frac B2=\frac\pi2-\frac C2$$

$$\cot\left(\frac A2+\frac B2\right)=\cot\left(\frac\pi2-\frac C2\right)=\tan\frac C2=\frac1{\cot\frac C2}$$

Apply $\cot(x+y)=\dfrac{\cot x\cot y-1}{\cot x+\cot y}$

Answer 3

Geometric Proof

Let $a,b,c$ be the length of the sides $BC,CA,AB$ respectively, $p$ be the semi-perimeter, $r$ be the radius of the incircle, and $S$ be the area.

Notice that $$\cot\frac{A}{2}=\frac{p-a}{r},~~~\cot\frac{B}{2}=\frac{p-b}{r},~~~\cot\frac{C}{2}=\frac{p-c}{r}.$$

Hence, $$\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2}=\frac{p}{r}.$$

and $$\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2}=\frac{(p-a)(p-b)(p-c)}{r^3}.$$

Recall Heron's formula $$S=\sqrt{p(p-a)(p-b)(p-c)},$$ and another area formula$$S=pr.$$ We obtain $$\frac{(p-a)(p-b)(p-c)}{r^3}=\frac{S^2}{pr^3}=\frac{(pr)^2}{pr^3}=\frac{p}{r}.$$

As a result, $$\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2}=\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2}.$$

Answer 4

Here’s a somewhat weird proof using inverse trigonometric functions

If $$A+B+C=π$$ then $$\frac{A}{2}+\frac{B}{2}+\frac{C}{2}=\frac{π}{2}$$

Let $$\frac{A}{2}=tan^{-1} x, \>\frac{B}{2}=tan^{-1} y ,\> \frac{C}{2}=tan^{-1} z$$ Now,

$$tan^{-1} x+ tan^{-1} y+ tan^{-1} z= π/2$$ $$tan^{-1} x+ tan^{-1} y= cot^{-1} z$$ Because $$tan^{-1} z+ cot^{-1} z= \frac{π}{2}$$ Now, $$tan^{-1} \frac{x+y}{1-xy}= cot^{-1} z$$ $$cot^{-1} \frac{1-xy}{x+y}= cot^{-1} z$$ $$\frac{1-xy}{x+y}=z$$ $$1=xy+yz+zx$$ $$\frac{1}{xyz}= \frac{1}{z}+ \frac{1}{x}+\frac{1}{y}$$ Now,we have $$cot \frac{A}{2} cot \frac{B}{2} cot \frac{C}{2}= cot \frac{C}{2}+cot \frac{A}{2}+cot \frac{B}{2}$$

Answer 5

It shouldn't be that hard cause you have this two.

$\frac{\cos (\frac{A}{2})}{\sin (\frac{A}{2})}+\frac{\cos (\frac{B}{2})}{\sin (\frac{B}{2})}+\frac{\cos (\frac{C}{2})}{\sin (\frac{C}{2})}=\frac{\cos (\frac{A}{2})}{\sin (\frac{A}{2})}\times \frac{\cos (\frac{B}{2})}{\sin (\frac{B}{2})}\times \frac{\cos (\frac{C}{2})}{\sin (\frac{C}{2})}$

$A+B+C=180$

Answer 6

Applying $\cot(x+y)=\dfrac{\cot x\cot y-1}{\cot x+\cot y}$ twice,

$$\cot(x+y+z)=\frac{\sum\cot x\cot y-1}{\prod\cot x-\sum\cot x}$$

Here $x=\dfrac A2$ etc. so that $x+y+z=\dfrac\pi2\implies\cot(x+y+z)=?$