Filter a specific area of an image

Question

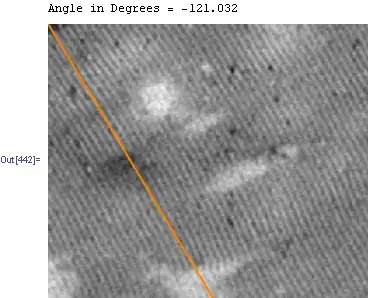
I try to obtain the angle of the periodic waves that you can see below.

I am using the FourierTransformation to get it:

direin = StringJoin[NotebookDirectory[], "Eingang\\"]; 
diraus = StringJoin[NotebookDirectory[], "Ausgang\\"];
SetDirectory[direin]; files = FileNames[{"*.png"}, FileNameJoin[{Directory[]}]] 
img = Import /@ FileNames[files[[1]]]; 
img = img[[1]]; 
img = ColorConvert[img, "Grayscale"]; 
(*sauberer FIltern*) 
noBorder = ImagePad[img, -BorderDimensions[img]]; 
{w, h} = ImageDimensions[noBorder]; 
wnd = Outer[Times, Array[HammingWindow, h, {-.5, .5}],     Array[HammingWindow, w, {-.5, .5}]];

rawPixels = ImageData[noBorder][[All, All, 1]]; 
imgTimesWnd = (rawPixels - Mean[Flatten[rawPixels]])*wnd; 
(*Fourier*) 
ft = Fourier[imgTimesWnd]; 
center = Floor[Dimensions[ft]/2]; 
ft = RotateRight[ft, center];

(*Winkel*) 
brightestOffset = First[Position[Abs[ft], Max[Abs[ft]]]] - center; 
maxAngle = ArcTan @@ N[brightestOffset/{h, w}]; 
getDeg = 180 / \[Pi]*maxAngle

It worked very well for a picture you can see here: Angle between two areas of an image of a 2D FFT

But for the picture you can see above i receive an image like this:

As you can see there are too many periodic reflections, so the code can't work.

My idea is to use a filter to get the interesting areas, marked as the area between the red circles in the image below.

Actually I tried a bandpass Filter and a Mask function... not very successful, do you have any other ideas?

Answer 1

Version 1 Using GradientOrientationFilter[ ]

i = Import["https://i.stack.imgur.com/HuyCnm.png"];
tvf = TotalVariationFilter[i, 1, Method -> "Laplacian", MaxIterations -> 100];
op = Closing[ImageSubtract[i, tvf] // Binarize, DiskMatrix[1]];
gof = ImageData[GradientOrientationFilter[op, 2]];
gof1 = ArcTan[Sin[gof], -Cos[gof]];
angle = Flatten@gof1 // Mean;
Print["Angle in Degrees = ", angle/Degree];
tan = Tan@angle;
Show[i, Graphics[{Orange, Thick, 
                  Line[Last@ImageDimensions[i] {{0, 1}, {1/tan, 0}}]}]]

Version 2 Using Radon[ ]

Another way, using the Radon Transform:

r = Radon[i];
lpl = LaplacianGaussianFilter[r, {5, 1}];
gf = GradientFilter[lpl, 3];
idr = ImageDimensions@gf;
cc = Ordering[Total@ImageData@gf, -5];
angles = cc Pi/First@idr;
t = angles // Mean // Tan; 
Show[i, Graphics[{Orange, Thick, 
   Line[Last@ImageDimensions[i] {{0, 1}, {-1/t, 0}}]}]]

Version 3 Patching your code

And here you have your code, adapted. Not much care taken, though.

img = Import["https://i.stack.imgur.com/HuyCnm.png"];
img = ColorConvert[img, "Grayscale"];

{w, h} = ImageDimensions[img];
wnd = Outer[Times, Array[HammingWindow, h, {-.5, .5}], 
   Array[HammingWindow, w, {-.5, .5}]];

rawPixels = ImageData[img];
imgTimesWnd = (rawPixels - Mean[Flatten[rawPixels]])*wnd;
(*Fourier*)
ft = Fourier[imgTimesWnd];
center = Floor[Dimensions[ft]/2];
fti = Image@Abs@RotateRight[ft, center];
ft1 = ImageData@ ColorConvert[
    ImageMultiply[ fti, Rasterize[Graphics[Rectangle[]], ImageSize -> 20]], 
                             "Grayscale"];

brightestOffset = First[Position[ft1, Max[ft1]]] - center;
t = ArcTan @@ N[brightestOffset/{h, w}]
Show[img, Graphics[{Orange, Thick, 
                   Line[Last@ImageDimensions[img] {{0, 1}, {1/t, 0}}]}]]