Is there a Graphics primitive for a cone without a base?

Question

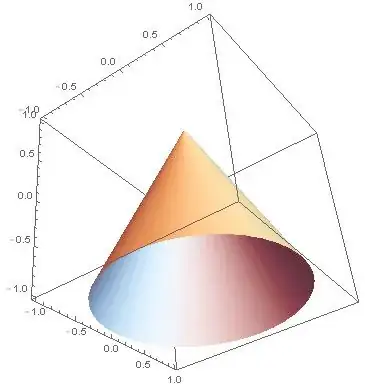
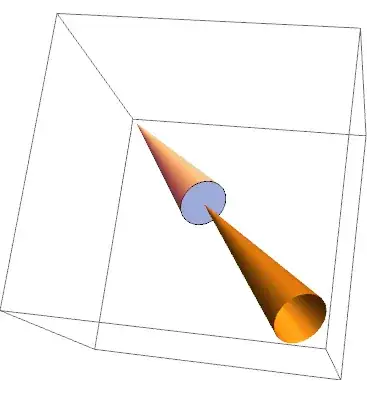
Is there an easy way to get a graphics primitive for a cone without a base without using RevolutionPlot3D? I'm trying to create an "manipulable" animation of the "space" and "body" cones for a body rotating in three dimensions (like the two animations at the bottom of the page here, but with adjustable parameters.) I've already created an animation like that using Cone objects, but their circular faces are always drawn, and I can't figure out how to tell Mathematica not to do that. (I'd rather not resort to revolution plots since this would require a massive overhaul of my code.)

In case you're curious: the code I have right now is a bit of a mess (in particular, it uses all sorts of special characters and subscripts, and so doesn't cut-and-paste well), but I can try to post it upon request.

I want this too, +1. I was looking for this not too long ago and came up empty-handed. — march, Dec 08 '15 at 22:31

score 15 · Accepted Answer · 2015-12-09T00:36:35.420

15

openCone[{{x1_, y1_, z1_}, {x2_, y2_, z2_}}, r_] := 
 {CapForm[None], Tube[{{x1, y1, z1}, {x2, y2, z2}}, {r, 0}]}

Graphics3D[openCone[{{0, 0, 1}, {1, 1, 0}}, 1]]

edited Dec 09 '15 at 00:36

answered Dec 08 '15 at 22:32

score 9 · Answer 2 · answered Dec 09 '15 at 02:46

I like Rahul's approach the most. An alternative way to produce open cones is to treat the cone as a NURBS surface:

openCone[{p1_?VectorQ, p2_?VectorQ}, r_?NumericQ] :=
    With[{tr = Composition[TranslationTransform[p1],
                           RotationTransform[{{0, 0, 1}, p2 - p1}]]}, 
         BSplineSurface[{tr /@ PadRight[r {{1, 0}, {1, 1}, {-1, 1}, {-1, 0},
                                           {-1, -1}, {1, -1}, {1, 0}},
                                        {Automatic, 3}], ConstantArray[p2, 7]}, 
                        SplineClosed -> {False, True}, SplineDegree -> {1, 2}, 
                        SplineKnots -> {{0, 0, 1, 1},
                                        {0, 0, 0, 1/4, 1/2, 1/2, 3/4, 1, 1, 1}},
                        SplineWeights ->
                        ConstantArray[{1, 1/2, 1/2, 1, 1/2, 1/2, 1}, 2]]]

With[{p1 = {0, 0, 1}, p2 = {1, 1, 0}, r = 1},
     {Graphics3D[openCone[{p1, p2}, r], Boxed -> False], 
      Graphics3D[Cone[{p1, p2}, r], Boxed -> False]} // GraphicsRow]

open and closed cones

score 4 · Answer 3 · answered Dec 08 '15 at 22:31

4

Graphics3D[Cone[],
 ClipPlanes -> {{0, 0, 1, 1}},
 Axes -> True]

answered Dec 08 '15 at 22:31

eldo

67,911
5
60
168

2

It may happen that there will be something more in Graphics3d :) – Kuba Dec 08 '15 at 22:32

score 3 · Answer 4 · edited Apr 13 '17 at 12:56

Just in case of Tube not being around. You won't have to change anything if you define syntax for your cone the same way the built in one is.

cone[{p1_, p2_}, r_] := GeometricTransformation[
  First @ RevolutionPlot3D[(-x/r + 1) Norm[p2 - p1], {x, 0, r}, 
            Mesh -> None, PerformanceGoal -> "Speed", PlotPoints -> 20],
  { RotationMatrix[{{0, 0, 1}, p2 - p1}], p1}
]


p1 = {1, 2, 1}
p2 = {2, 3, 2}
r = .2
Graphics3D[{
  cone[{p1, p2}, r]
  ,
  Translate[Cone[{p1, p2}, r], {1, 1, 1}]
  },
 BoxRatios -> Automatic]

ref: Change position and orientation of 3D object

Is there a Graphics primitive for a cone without a base?

4 Answers4

Linked