Get Graphics3D object for only part of a cone

Question

I have the necessary information to define a cone and plot it in Mathematica:

Rc = 0.38663124715321806`;
cvec = {0.9549268454424656`, 
   0.693794964347954`, -0.18315267078439607`};
openCone[{{x1_, y1_, z1_}, {x2_, y2_, z2_}}, r_] := {CapForm[None], 
  Tube[{{x1, y1, z1}, {x2, y2, z2}}, {r, 0}]}
cone = Graphics3D[{openCone[{cvec, {0, 0, 0}}, Rc]}];

where I have used the openCone[] defined here: Is there a Graphics primitive for a cone without a base?

This is all good. Now I would like to go one step further. I have the locations of two vectors lying on the cone:

tvec1={1.15282, 0.490827, 0.0797662};
tvec2={0.823045, 0.944722, 0.0797662};

Plotting everything together,

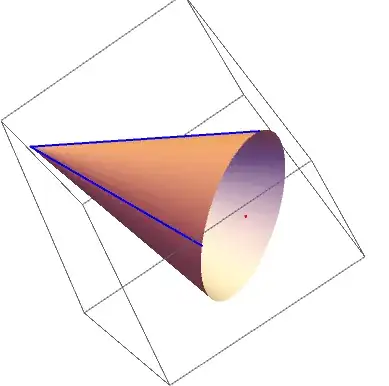
Show[cone,
 Graphics3D[{Thick, Blue, Line[{{0, 0, 0}, tvec1}], 
   Line[{{0, 0, 0}, tvec2}], 
   {Red, Point[cvec]}}]
 ]

I get the picture:

Now, what I want to do is plot only the section of the cone that lies between the two blue lines (make a Graphics3D object)-- let's say the smaller section. How would I do that?

The simplest theoretical approach that I can think of is to define the plane comprised of tvec1, tvec2 and {0,0,0}, and plot only the 'points' that lie above (or below) the plane. But I have no idea how to implement this, especially since all I have is a Graphics3D object. Please help.

---

ADDENDUM: Why I am asking for a new Graphics3D object ...

I want more than just to display part of the cone (hence, an option like ClipPlanes doesn't suffice). I want a new Graphics3D object so that I can do other operations with it.

In particular, I have a collection of many of these cones and other Graphics3D objects pieced together, and I want to apply the smoothing procedures GraphDiffusionFlow[] and MeanCurvatureFlow[] to the whole complex (defined here: Smoothing 3D contours as post processing).

My understanding is that I need a meshed surface for applying these functions, hence my request for a Graphics3D object so that I can use something like DiscretizeGraphics[]. As mentioned in a comment, the current definition of openCone doesn't support DiscretizeGraphics[] since contains a Tube. So I need an alternative.

Answer 1

We construct a space circle by

 cvec + Rc*(Cos[t]*e1 + Sin[t]*e2)

and then extrude the point o={0,0,0} to this circle to construct the cone.

s*o + (1 - s)*(cvec + Rc*(Cos[t]*e1 + Sin[t]*e2))

At the end, we use the two lines tvec1 and tvec2 to define a half space to separated the two part of cone.

HalfSpace[sign*Cross[tvec1 - o, tvec2 - o], o]

Rc = 0.38663124715321806`;
cvec = {0.9549268454424656`, 
   0.693794964347954`, -0.18315267078439607`};
tvec1 = {1.15282, 0.490827, 0.0797662};
tvec2 = {0.823045, 0.944722, 0.0797662};
o = {0, 0, 0};
{v1, v2, v3} = # & /@ HodgeDual[cvec - o];
e1 = Normalize[v1];
e3 = Normalize[cvec - o];
e2 = Cross[e1, e3];
Table[ParametricPlot3D[
  s*o + (1 - s)*(cvec + Rc*(Cos[t]*e1 + Sin[t]*e2)), {t, 0, 
   2 π}, {s, 0, 1}, Boxed -> False, Axes -> False, Mesh -> None, 
  RegionFunction -> 
   Function[{x, y, z}, 
    RegionMember[
     HalfSpace[sign*Cross[tvec1 - o, tvec2 - o], o], {x, y, 
      z}]]], {sign, {1, -1}}]

Answer 2

We may draw a piece of a cone using ParametricPlot3D. Toward this end, we redefine the function openCone.

We need following data: the point at the base: pbase and at the tip: ptip of the cone. Then we need two points: pts on the base circle, defining the start and the end of the cone section. Finally we need the radius: r of the base.

For the cone section we define a function cir[phi_] that returns the point on the base circles that, together with the center, defines a line that makes an angle of phi with line from the base center in x direction.. We further define angle[v1_v2_] that returns the angle between 2 3D vectors. With the help of these 2 function we can create a plot of the cone section.

openCone[{p1_, p0_}, {p2_, p3_}, r_] := 
  Module[{cir, ph2, ph3, n = Normalize[p0 - p1], t, q0, qx, qy, qz}, 
   cir[ph_] := p1 + r  RotationMatrix[ph, n].q0;
   angle[v1_, v2_] := (t = ArcTan[v1.v2, Cross[v1, v2].n]; 
     If[t < 0, 2 Pi + t, t]);
   {qx, qy, qz} = pbase - ptip;
   q0 = If[qx == qy == 0, {1, 0, 0}, {-qy, qx, 0}/Sqrt[qx^2 + qy^2]];
   ph2 = angle[q0, p2 - p1];
   ph3 = angle[q0, p3 - p1];
ParametricPlot3D[p0 + l (cir[ph] - p0), {l, 0, 1}, {ph, ph2, ph3}, 
    BoxRatios -> Automatic]];

Here is an example:

pbase = {1, 0, 0}; ptip = {1., 1, 1}; r = 1;
{qx, qy, qz} = pbase - ptip;
q0 = If[qx == qy == 0, {r, 0, 0}, r {-qy, qx, 0}/Sqrt[qx^2 + qy^2]];
pts = ({pbase +  RotationMatrix[p1, ptip - pbase].q0, 
     pbase + RotationMatrix[p2, ptip - pbase].q0} /. {p1 -> 0, 
     p2 -> Pi 5/4});
Show[t = openCone[{pbase, ptip}, pts, r], 
 Graphics3D[{Blue, Thickness[0.01], 
   Line[{{ptip, pts[[1]]}, {ptip, pts[[2]]}}], PointSize[0.02], 
   Point[pts]}], Axes -> True, AxesLabel -> {"x", "y", "z"}]