1

I've been trying to solve the following equations in order to plot Subscript[θ, 41] with respect to Subscript[θ, 2] from 0 to 360 degrees.

enter image description here

Subscript[r, 1] = 38.79;
Subscript[r, 2] = 15;
Subscript[r, 3] = 50;
Subscript[r, 41] = 41.5;
Subscript[θ, 1] = 191.6 Degree;

Eq1 = Subscript[r, 1] Cos[Subscript[θ, 1]] == 
        (Subscript[r, 2] Cos[Subscript[θ, 2] \[Degree]] + 
         Subscript[r, 3] Cos[Subscript[θ, 3] \[Degree]] + 
         Subscript[r, 41] Cos[Subscript[θ, 41] \[Degree]])

Eq2 = Subscript[r, 1] Sin[Subscript[θ, 1]] == 
        (Subscript[r, 2] Sin[Subscript[θ, 2] \[Degree]] + 
         Subscript[r, 3] Sin[Subscript[θ, 3] \[Degree]] + 
         Subscript[r, 41] Sin[Subscript[θ, 41] \[Degree]])

Plot[(Subscript[θ, 41] /. 
        NSolve[{Eq1, Eq2}, {Subscript[θ, 3], Subscript[θ, 41]}][[2]]) + 360, 
        {Subscript[θ, 2], 0, 360} , PlotRange -> {{0, 360}, {240, 300}}]

Solution = (Subscript[θ, 41] /. 
        NSolve[{Eq1, Eq2}, {Subscript[θ, 3], Subscript[θ, 41]}][[2]]) + 360;

Plot[Solution, {Subscript[θ, 2], 0, 360}]

The solution of this gives 4 solutions for Subscript[θ, 41]. The problem is, whenever I try to plot one of those solutions by putting the whole Solve phrase in the Plot statement, it works. But whenever I try to do them separately, it gives a completely different plot.

More details shown in the following photos:

enter image description here

The first plot is the one I'm looking for. The second one gives a different plot!... Although I technically haven't done anything different.

I think it's important to mention that I've noticed that the strange plot I got (the second one) is somehow a combination of all 4 solutions. It's typical to a certain solution in a certain range of Theta's, then flips to another solution in another range. I don't know how this helps.

I hope someone would explain this to me, thank you !!

Abdelrahman Fikry Elashry
  • 11
  • 2
  • Please add your code in a copyable format instead or in addition to the picture. – Karsten7 Dec 11 '15 at 21:35
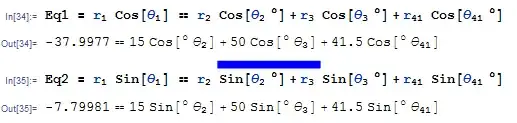
  • Possibly the two plots are different due to the fact that Plot has attribute HoldAll or that it effectively is using Block for Theta2. – Karsten7 Dec 11 '15 at 21:37
  • @Karsten7. I've added my code at the top of my post. – Abdelrahman Fikry Elashry Dec 11 '15 at 21:56
  • @Karsten7. The point is, I can't keep plugging in all my Nsolve[] statements in my plots, my code gets messier and I end up using nested Nsolve statements which takes Mathematica ages to plot, I need to save my Theta41 solution somewhere to use it later on instead of having to generate it every time, But as you can see, It doesn't give the same solution when I try to plot it after being saved :/ .. Suggestions? Thanks! – Abdelrahman Fikry Elashry Dec 11 '15 at 22:09
  • Subscript[r, 3 ] is undefined. Is that intentional? – bbgodfrey Dec 11 '15 at 23:36
  • @bbgodfrey That probably should be Subscript[r, 3] = 50. – Karsten7 Dec 11 '15 at 23:51
  • There seems to be other parts of the code missing. Can't reproduce the second plot evaluating the given code. – Karsten7 Dec 11 '15 at 23:53
  • @Karsten7. Agree on both counts. Moreover, code for two plots look equivalent to me, and I do not understand how the code for the first plot produces anything. – bbgodfrey Dec 12 '15 at 00:03
  • @Karsten7. Yes I missed that line, apologies i added it. – Abdelrahman Fikry Elashry Dec 12 '15 at 00:16
  • 1
    @bbgodfrey The first plot produces something, because Subscript[\[Theta], 2] has a value at every point Plot evaluates that NSolve[...]. It is very similar to the situation here. – Karsten7 Dec 12 '15 at 00:17
  • @Karsten7.You were right about the HoldAll attribute, I tried holding ( Solution ), Then Releasing it inside the plot statement, The output was the same as the initial plot, which is the correct one. This, though, doesn't solve the problem of the fact that I have to evaluate all of my solve statements inside my plots, It slows down my plotting. – Abdelrahman Fikry Elashry Dec 12 '15 at 00:21
  • You should avoid using Subscript while defining symbols (variables). Subscript[x, 1] is not a symbol, but a compound expression where Subscript is an operator without built-in meaning. You expect to do $x_1=2$ but you are actually doing Set[Subscript[x, 1], 2] which is to assign a Downvalue to the oprator Subscript and not an Ownvalue to an indexed x as you may intend. Read how to properly define indexed variables here – rhermans Feb 22 '16 at 10:17
  • 1
    I'm voting to close this question as off-topic because it is too localized; i.e, it applies only to the local situation and needs of its poster and answers will not benefit others. – m_goldberg Feb 22 '16 at 15:45

0 Answers0