5

I am experiencing strange behavior within Mathematica when plotting the InverseLaplaceTransform of a function. Essentially, I get a different plot when I paste in the result of the InverseLaplaceTransform evaluation than I do if I just plot the function that involves the InverseLaplaceTransform.

I may not have explained this very well, but hopefully the example code that I have pasted below will clear things up.

EDIT: as pointed out in the comments, there was a typo in the code. See below. Regardless, the issue is still present.

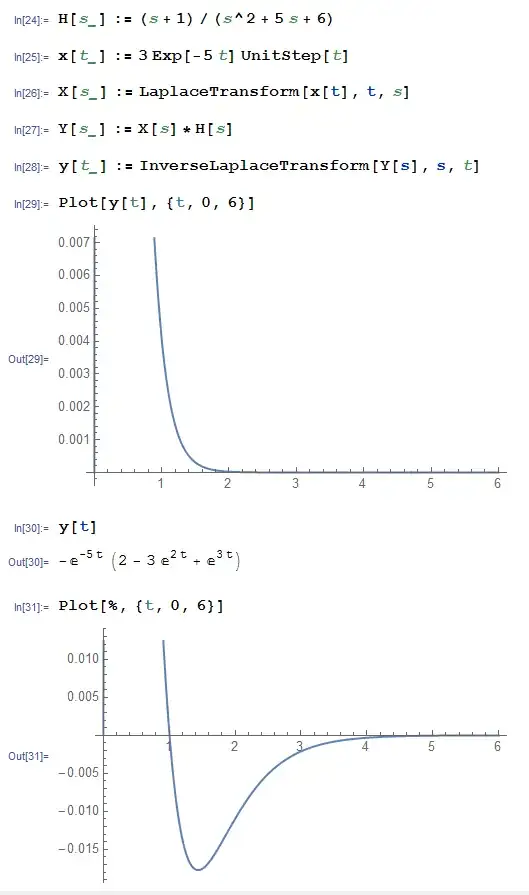
H[s_] := (s + 1)/(s^2 + 5 s + 6)
x[t_] := 3 Exp[-5 t] UnitStep[t]

(* X[s_] := LaplaceTransform[xb2[t], t, s] *)
X[s_] := LaplaceTransform[x[t], t, s]

Y[s_] := X[s]*H[s]
y[t_] := InverseLaplaceTransform[Y[s], s, t]
Plot[y[t], {t, 0, 6}]
y[t]
Plot[%, {t, 0, 6}]

If you run this code, you should observe that the two plots are quite different. I was expecting them to be identical, but perhaps I have overlooked something. I have included a screen capture of my results below.

(Updated) Screenshot of my results

rhermans
  • 36,518
  • 4
  • 57
  • 149
Peter Crowley
  • 181
  • 4

1 Answers1

8
H[s_] := (s + 1)/(s^2 + 5 s + 6)
x[t_] := 3 Exp[-5 t] UnitStep[t]
X[s_] := LaplaceTransform[x[t], t, s]
Y[s_] := X[s]*H[s]

Clear[y]

y[t_] := InverseLaplaceTransform[Y[s], s, t]

?y

enter image description here

Since y is defined with SetDelayed and Plot has the attribute HoldAll, you need to Evaluate it within the Plot

Attributes[Plot]

(*  {HoldAll, Protected, ReadProtected}  *)

Plot[Evaluate[y[t]], {t, 0, 6}, PlotRange -> All]

enter image description here

Alternatively, define y with Set

Clear[y]

y[t_] = InverseLaplaceTransform[Y[s], s, t];

?y

enter image description here

Note that the stored definition of y is the evaluation of the InverseLaplaceTransform

Plot[y[t], {t, 0, 6}, PlotRange -> All]
Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • @"Bob Hanlon" - I see the result but don't fully understand it. I would think that not using Evaluate would be extremely slow. I would expect that InverseLaplaceTransform would be repeatedly evaluated for each point. Yet I would still expect the answer to be correct. Can you elaborate as to why we actually get an incorrect plot? Thank you – Jack LaVigne Nov 07 '15 at 17:33
  • @JackLaVigne - as shown in the edit above, when y is defined with Set the stored definition is the evaluated InverseLaplaceTransform so the Plot is not significantly slowed by not using Evaluate. I do not know why the plot is wrong rather than just slowed when y is defined with SetDelayed and not evaluated within the Plot. – Bob Hanlon Nov 07 '15 at 21:15
  • 1
    @JackLaVigne The reason for the incorrect Plot is that Plot effectively uses Block. Compare for example y[1.5] with Block[{t = 1.5}, y[t]]. There is a global t in X, which also gets effected when Block is used. – Karsten7 Nov 07 '15 at 21:27
  • @Karten7 - Thank you for the explanation. I think I get it. – Jack LaVigne Nov 07 '15 at 23:41