I have a problem with the DSolve[] command in mathematica 8. Solving the the following 4th order differential equation spits out a complex solution although it should be a real one. The equation is:
y''''[x] + a y[x] == 0
Solving this equation by hand yields a solution with only real parts. All constants and boundary conditions are also real numbers.
The solution I get by hand is:
y1[x_] = (C[5] E^(Power[a, (4)^-1]/Power[2, (2)^-1] x) +
C[6] E^(-(Power[a, (4)^-1]/Power[2, (2)^-1]) x)) Cos[
Power[a, (4)^-1]/Power[2, (2)^-1]
x] + (C[7] E^(Power[a, (4)^-1]/Power[2, (2)^-1] x) +
C[8] E^(-(Power[a, (4)^-1]/Power[2, (2)^-1]) x)) Sin[
Power[a, (4)^-1]/Power[2, (2)^-1] x];
Now I have to solve for the constants C[5]...C[8]. This arises a similar issue. I use the Solve[] command with the boundary conditions
Solve[{y1''[-c] == ic0, y1''[c] == ic0 , y1'''[-c] == ic1 ,
y1'''[c] == - ic1 }, {C[5], C[6], C[7], C[8]} ];
The constants C[5]...C[8] are now real if using //Simplify and complex if using //FullSimplify.
Any idea what the reasons are? The notebook with my calculations can be downloaded under: http://dl.dropbox.com/u/4920002/DGL_4th_Order_with_own_solution.nb
In further work I have to use DSolve[] and I would like to understand the issue here.
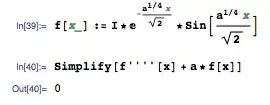



DSolve[]always treats all variables as complex; unless you tell, say,FullSimplify[]thatais real, you'll get the complex bits. 2. You've noticed that the characteristic equation of your DE has complex roots, yes?