Suppose the function
SingleCrossSection[Ss_, s2_, m_, m2_, mp_] =
-(1/(288 π^3 s2^3 Ss^4 (mp^2 - Ss)^2))
((m^2 - s2) (1/((m + m2)^2 - (mp - Sqrt[
Ss])^2) (s2 - (mp - Sqrt[
Ss])^2) Sqrt[-2 mp^2 ((m + m2)^2 + Ss) + ((m + m2)^2 -
Ss)^2 +
mp^4] (m^4 (-6 mp^8 + 3 mp^6 (s2 + 24 Ss) +
mp^4 (3 s2^2 - 27 s2 Ss - 172 Ss^2) +
mp^2 Ss (-30 s2^2 - 19 s2 Ss + 152 Ss^2) +
Ss^2 (35 s2^2 + 35 s2 Ss - 46 Ss^2)) +
m^2 s2 (3 mp^8 - 6 mp^6 (s2 + 12 Ss) +
mp^4 (3 s2^2 + 18 s2 Ss + 110 Ss^2) -
2 mp^2 Ss (15 s2^2 + 17 s2 Ss + 8 Ss^2) +
Ss^2 (11 s2^2 + 38 s2 Ss - 25 Ss^2)) -
s2^2 (-3 mp^8 - 3 mp^6 (s2 - 24 Ss) +
mp^4 (6 s2^2 + 63 s2 Ss - 134 Ss^2) +
mp^2 Ss (-60 s2^2 + 19 s2 Ss + 64 Ss^2) +
Ss^2 (46 s2^2 - 71 s2 Ss + Ss^2))) +
12 Ss^2 (m^4 (2 mp^6 - 3 mp^4 (s2 + 2 Ss) + 6 mp^2 Ss^2 +
s2^3 + 3 s2 Ss^2 - 2 Ss^3) +
m^2 s2 (2 mp^6 + 3 mp^4 (s2 - 2 Ss) -
6 mp^2 (s2^2 + s2 Ss - Ss^2) + s2^3 + 3 s2 Ss^2 -
2 Ss^3) +
s2^2 (-mp^6 + 3 mp^4 (s2 + Ss) - 3 mp^2 Ss^2 - 2 s2^3 +
6 s2^2 Ss - 3 s2 Ss^2 + Ss^3)) Log[-(
s2/(-2 mp^2 + 4 mp Sqrt[Ss] + s2 - 2 Ss))]) -
12 Ss^2 Log[
m2^2/(-m^2 - 2 m m2 +
s2)] (-3 s2^3 (mp^2 - Ss)^2 (m^2 + mp^2 - Ss) Log[-(
s2/(-2 mp^2 + 4 mp Sqrt[Ss] + s2 - 2 Ss))] -
1/((m + m2)^2 - (mp - Sqrt[Ss])^2) (m^2 -
s2) (s2 - (mp - Sqrt[
Ss])^2) Sqrt[-2 mp^2 ((m + m2)^2 + Ss) + ((m + m2)^2 -
Ss)^2 +
mp^4] (m^4 (-2 mp^4 + mp^2 (s2 + 4 Ss) + s2^2 + s2 Ss -
2 Ss^2) +
m^2 s2 (-2 mp^4 + mp^2 (4 Ss - 5 s2) + s2^2 + s2 Ss -
2 Ss^2) +
s2^2 (mp^4 - 2 mp^2 (s2 + Ss) - 2 s2^2 + 4 s2 Ss +
Ss^2))));
defined on
{s2, (m+m2)^2, (Sqrt[Ss]-mp)^2}, Ss > (mp+m2+m)^2, m > 0, m2>0, mp>0
It is real function of its arguments on the domain of the definition.
I'm trying to evaluate its integral over s2:
CrossSectionIntegral[Ss_, s2_, m_, m2_, mp_] =
Simplify[Integrate[SingleCrossSection[Ss, s2, m, m2, mp],
s2, Assumptions -> Ss > 0 && Sqrt[Ss] > mp + m2 + m]];
CrossSection[Ss_, m_, m2_, mp_] =
Collect[CrossSectionIntegral[Ss, (Sqrt[Ss]-mp)^2, m, m2, mp] -
CrossSectionIntegral[Ss, (m+m2)^2, m, m2, mp], m] ;
The huge output for the integration contains, as far I can see, the combinations of polylogarithms with positive arguments larger than 1 and logarithms with negative arguments, and thus seems to be comples. However, because of an identity relating a polylogarithm with the argument larger than one with a polylogarithm with the argument less than one, all the imaginary terms becomes zero. Mathematica seems to know these identities, or at least evaluates the imaginary part to zero.
Now, I'm going to check this graphically for particular values of Ss, mp,m2. I write
Plot[{CrossSection[6.5, m, 0.1, 1]}, {m, 0, Sqrt[6.5] - 1}]
The output is not smooth, there are some discontinuites on the plot (the yellow curve, please ignore the blue curve here and below):

From the other side, if I plot the real part,
Plot[{Re[CrossSection[6.5, m, 0.1, 1]]}, {m, 0, Sqrt[6.5] - 1}]
the graphic is the same, but discontinuites are lost (the yellow curve):
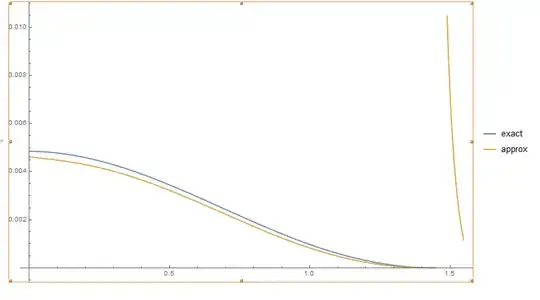
Please ignore any errors during obtaining the output (such as "Infinite expression 1/0 encountered"), since the reason for them is just slightly incorrect upper limit for the plot (it must be smaller).
What can be the reason of such problem? I expect that the integral of the function over the domain where it is real and continuous will be real quantity, so it seems that the problem may be in misinterpretation of the output by Mathematica.

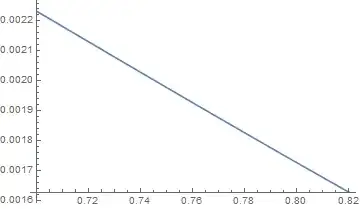
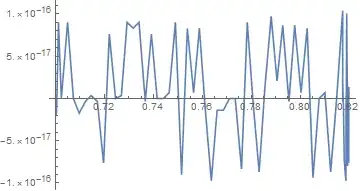
PlotPoints? Have I understood the question; are the discontinuities the problem of the appearance or another curve when you take the real part? – Hugh Aug 07 '17 at 17:13PlotPoints-> 500. This will give 500 starting points and this may find all the intervals. – Hugh Aug 07 '17 at 17:19Plotto avoid imaginary artifacts. Use the optionWorkingPrecision. To ensure that the input (CrossSection) supports the requestedWorkingPrecisionyou should use either exact numbers or high precision numbers for the arguments ofCrossSection. If using high precision arguments toCrossSection, the specified precision must be higher than theWorkingPrecisionsince some precision is lost in calculatingCrossSection. For example, withWorkingPrecion->20use numbers like 6.5`25 – Bob Hanlon Aug 07 '17 at 19:03