I have troubles substituting functions when I have symbolic derivatives and I need to substitute more symbolic derivatives in my expression. Take for example
D[f[x, y], {x, 2}];
% /. f[x, y] -> x^2 h[x, y]
The output is
(f^(2,0))[x,y]
and not $x^2\, \partial_x^{\,2}h(x,y)+4\,\partial_x h(x,y) x + 2\, h(x,y)$.
While I've read that this happens because
D[f[x, y], {x, 2}] // FullForm
gives
Derivative[2, 0][f][x, y]
and f[x, y] is not present here anymore, I couldn't find a solution for this.
Any ideas?

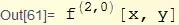



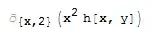

D[x h[x, y], {x, 2}]to see. btw, it might be easier just to make a function.r[expr_] := D[expr, {x, 2}];then you can dor[f[x, y]]andr[x h[x, y]]– Nasser Jan 31 '16 at 11:20% /. f -> (#^2 h[#, #2] &)– Kuba Jan 31 '16 at 11:58