I've put this code on a GitHub but I don't know what features are needed or what problems it may give. I'm just not using it.
But I will incorporate incomming suggestions as soon as I have time.
Feedback in form of tests and suggestions very appreciated!
(If[DirectoryQ[#], DeleteDirectory[#, DeleteContents -> True]];
CreateDirectory[#];
URLSave[
"https://raw.githubusercontent.com/" <>
"kubaPod/MoreCalculus/master/MoreCalculus/MoreCalculus.m"
,
FileNameJoin[{#, "MoreCalculus.m"}]
]
) & @ FileNameJoin[{$UserBaseDirectory, "Applications", "MoreCalculus"}]
https://github.com/kubaPod/MoreCalculus
So this is a package MoreCalculus` with the function DChange inside.
What's new:
DChange automatically takes under consideration range assumptions for built-in transformations: (not heavily tested)
DChange[
D[f[x, y], x, x] + D[f[x, y], y, y] == 0,
"Cartesian" -> "Polar", {x, y}, {r, θ}, f[x, y]
]

Usage:
DChange[expresion, {transformations}, {oldVars}, {newVars}, {functions}]
DChange[expresion, "Coordinates1"->"Coordinates2", ...]
DChange[expresion, {functionsSubstitutions}]
You can also skip {} if a list has only one element.
Examples:
Change of coordinates
rules accepted by CoordinateTransform are now incorporated, as well as coordinates ranges assumptions associated with them
DChange[
D[f[x, y], x, x] + D[f[x, y], y, y] == 0,
"Cartesian" -> "Polar", {x, y}, {r, θ}, f[x, y]
]

The transformation is returned too, to check if the canonical (in MMA) order of variables was used.
wave equation in retarded/advanced coordinates
DChange[
D[u[x, t], {t, 2}] == c^2 D[u[x, t], {x, 2}]
,
{a == x + c t, r == x - c t}, {x, t}, {a, r}, {u[x, t]} ]
c Derivative[1, 1][u][a, r] == 0
stereographic projection
DChange[
D[η*D[f[η], η], η]/η + (1 - s^2/η^2)*f[η] - f[η]^3 == 0
,
η == Sqrt[(1+z)/(1-z)], η, z, f[η] ]
((z-1)^2 (z+1)((z^2-1) f''[z]+2 z f'[z])-f[z] (s^2 (z-1)+z+1)+(z+1) f[z]^3)/(z+1)==0
Example from @Takoda
$$
\begin{pmatrix}\dot{x}\\
\dot{y}
\end{pmatrix}=\begin{pmatrix}-y\sqrt{x^{2}+y^{2}}\\
x\sqrt{x^{2}+y^{2}}
\end{pmatrix}
$$
out = DChange[
Dt[{x, y}, t] == {-y r^2, x r^2}, "Cartesian" -> "Polar",
{x, y}, {r, θ}, {}
]
Solve[out[[1]], {Dt[r, t], Dt[θ, t]}]
{{Dt[r, t] -> 0, Dt[θ, t] -> r^2}}
Functions replacement
example on special case separation of Fokker-Planck equation
DChange[
-D[u[x, t], {x, 2}] + D[u[x, t], {t}] - D[x u[x, t], {x}]
,
u[x, t] == Exp[-1/2 x^2] f[x] T[t]
] // Simplify
% / Exp[-x^2/2] / f[x] / T[t] // Expand

Code: (latest version is on GitHub)
ClearAll[DChange];
DChange[expr_, transformations_List, oldVars_List, newVars_List, functions_List] :=
Module[ {pos, functionsReplacements, variablesReplacements, arguments,
heads, newVarsSolved}
,
pos = Flatten[
Outer[Position, functions, oldVars],
{{1}, {2}, {3, 4}}
];
heads = functions[[All, 0]];
arguments = List @@@ functions;
newVarsSolved = newVars /. Solve[transformations, newVars][[1]];
functionsReplacements = Map[
Function[i,
heads[[i]] -> (
Function[#, #2] &[
arguments[[i]],
ReplacePart[functions[[i]], Thread[pos[[i]] -> newVarsSolved]]
] )
]
,
Range @ Length @ functions
];
variablesReplacements = Solve[transformations, oldVars][[1]];
expr /. functionsReplacements /. variablesReplacements // Simplify // Normal
];
DChange[expr_, functions : {(_[___] == _) ..}] := expr /. Replace[
functions, (f_[vars__] == body_) :> (f -> Function[{vars}, body]), {1}]
DChange[expr_, x___] := DChange[expr, ##] & @@ Replace[{x},
var : Except[_List] :> {var}, {1}];
DChange[expr_, coordinates:Verbatim[Rule][__String], oldVars_List,
newVars_List, functions_ ]:=Module[{mapping, transformation},
mapping = Check[
CoordinateTransformData[coordinates, "Mapping", oldVars],
Abort[]
];
transformation = Thread[newVars == mapping ];
{
DChange[expr, transformation, oldVars, newVars, functions],
transformation
}
];
TODO:
- add some user friendly
DownValues for simple cases
- heavy testing needed, feedback appreciated
- exceptions/errors handling. it is only as powerful as
Solve so may brake for more convoluted implicit relations
- it is not designed as a scoping construct


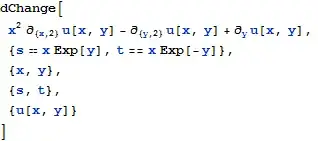


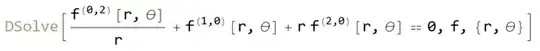


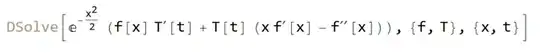
ReplaceandReplaceAllare more than enough and, actually, I found them much powerful than Maple'sdchange. – m0nhawk Apr 18 '15 at 08:37Assumptionsoption in thedChangeemulation to tell Mathematica which variables are positive, or complex, etc... so it has a better chance of inverting and simplifying the required relations. Anyway, I like the idea... – Jens Apr 18 '15 at 16:32