Brackets around each item in matrix

Question

I have a matrix where every item in the matrix has its own brackets that I do not want. How can I remove the brackets around each item?

Answer 1

Wrap the matrix rows with the the Flatten function

M = {{{1}, {2}, {3}, {4}}, {{5}, {6}, {7}, {8}}}

To save time you can wrap your whole matrix using: Map[Flatten, <yourmatrix> ]

Map[Flatten,{{{1}, {2}, {3}, {4}}, {{5}, {6}, {7}, {8}}}]

the outermost list contains two elements (the rows). the Map function wraps these elements with the Flatten function

{{1, 2, 3, 4}, {5, 6, 7, 8}}

In Mathematica this is known as "nested" Lists. Flatten removes all wrappings of the List function until only one remains

To understand what the Map function does: Below is the "manual" approach without the Map function.

{  
 Flatten[{{1}, {2}, {3}, {4}}],

 Flatten[{{5}, {6}, {7}, {7}}]
}

As you are talking to an awesome machine called the Mathematica kernel you don't have to waste time writing things in long hand to make them readable (like you would for a slow-to-understand human reader of an essay or your future self reading your code).

hence Map[Flatten, Matrix] has the terse shorthand form Flatten /@ matrix

mentioned by @garej , @jjc385 and @Mr.Wizard below

Answer 2

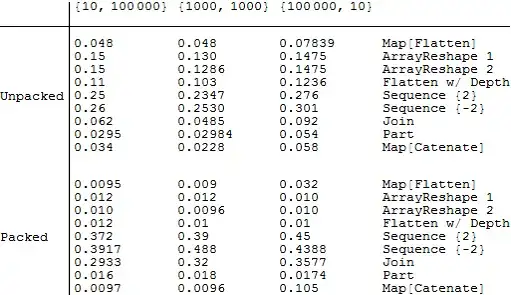
Lots of solutions. Time for a benchmark. My own contribution is Part:

m = {{{1}, {2}, {3}}, {{2}, {4}, {6}}};

m[[All, All, 1]];

{{1, 2, 3}, {2, 4, 6}}

Update: I made a complete mess of my earlier attempt at benchmarking. Here is a rewrite.

methods = Hold[Flatten /@ m, ArrayReshape[m, Most@Dimensions@m], 
   ArrayReshape[m, Dimensions[m][[1 ;; 2]]], Flatten[m, {Depth[m] - 1, 1}], 
   Apply[Sequence, m, {2}], Apply[Sequence, m, {-2}], Join @@@ m, m[[All, All, 1]], 
   Catenate /@ m];

names = {"Map[Flatten]", "ArrayReshape 1", "ArrayReshape 2", "Flatten w/ Depth", 
   "Sequence {2}", "Sequence {-2}", "Join", "Part", "Map[Catenate]"};

upk[{x_, y_}] := Table[{ToString[i*j]}, {i, x}, {j, y}];
pkd[{x_, y_}] := RandomReal[1, {x, y, 1}];

tab = 
 Table[
  List @@ First /@ RepeatedTiming /@ methods,
  {fn, {upk, pkd}},
  {shape, {{10, 100000}, {1000, 1000}, {100000, 10}}},
  {m, {fn[shape]}}
 ];

TableForm[
  Append[names] /@ (tab //. {x_List} :> x),
  TableHeadings -> {{"Unpacked", "Packed"}, {{10, 100000}, {1000, 1000}, {100000, 10}}},
  TableSpacing -> {5, 1, 0.5}
]

(Benchmark timings in 10.1.0 under Windows 7 x64.)

It seems that in most instances Part wins, but a few times Catenate edges it out.

Answer 3

You can use ArrayReshape. Either

ArrayReshape[mat, Most@Dimensions@mat]

or

ArrayReshape[mat, Dimensions[mat][[1 ;; 2]]]

It will keep a packed array packed, too.

Answer 4

Edit With m = RandomInteger[9, {3, 6, 1}]

Just for completeness:

Catenate /@ m

---

Just for diversity reasons

Apply[#&, m, {2}]
Apply[Sequence, m, {-2}]
Map[First, m, {2}]

Using @Mr.Wizard code I have updated the benchmark.

@MichaelE2 also noticed in comments that Catenate is not compilable.

Answer 5

You can also Apply Join at level 1 to your list:

m = RandomInteger[9, {2, 4, 1}]

{{{0}, {6}, {7}, {5}}, {{1}, {3}, {8}, {8}}}

Join @@@ m

{{0, 6, 7, 5}, {1, 3, 8, 8}}

Answer 6

I suggest Flatten[m, {Depth[m] - 1, 1}], where m is the matrix in question.

For example,

SeedRandom[1]; m = RandomInteger[99, {4, 5, 1}]

{{{80}, {14}, {0}, {67}, {3}}, 
 {{65}, {23}, {97}, {68}, {74}}, 
 {{15},{24}, {4}, {90}, {83}}, 
 {{70}, {1}, {30}, {48}, {25}}}

Flatten[m, {Depth[m] - 1, 1}]

{{80, 14, 0, 67, 3}, 
 {65, 23, 97, 68, 74}, 
 {15, 24, 4, 90, 83}, 
 {70, 1, 30, 48, 25}}

Answer 7

...and of course, there's always Transpose[]:

Transpose[{{{1}, {2}, {3}}, {{2}, {4}, {6}}}, {2, 3, 1}] // First
   {{1, 2, 3}, {2, 4, 6}}

The Flatten[] equivalent is then

Flatten[{{{1}, {2}, {3}}, {{2}, {4}, {6}}}, {{1}, {3, 2}}]
   {{1, 2, 3}, {2, 4, 6}}