How would I plot $x^2+y^2=1$ in 3D (it would form a cylinder)? Since there is no $z$ in the equation, I can't solve for it and use Plot3D. Or can I just put the equation into Plot3D? I am very new to Mathematica.
Asked
Active
Viewed 2.5k times
7
diracdeltafunk
- 215
- 1
- 2
- 7
2 Answers
14
How about a 3D contour plot.
ContourPlot3D[x^2 + y^2 == 1, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]
Mark McClure
- 32,469
- 3
- 103
- 161
-
Oh, great! Thanks! – diracdeltafunk Sep 16 '12 at 22:52
-
No problem! Have fun Ben. – Mark McClure Sep 16 '12 at 22:54
11
Although Mark's answer is the "natural" one, here are other options just for completeness:
Use Plot3D, after performing a rotation:
Plot3D[{1, -1} Sqrt[1 - x x], {x, -1, 1}, {y, -1, 1}, AspectRatio -> 1]

Use ParametricPlot3D[]:
ParametricPlot3D[{{1, -1, 1} #, {1, 1, 1} #} &@{x, Sqrt[1 - x x], z}, {x, -1, 1}, {z, 0, 1}]

Use RevolutionPlot3D[] after realizing for example that in the semi/plane {y==0, x>0} x takes only the value 1 and z takes any value (freely):
RevolutionPlot3D[{1, t}, {t, 0, 1}]
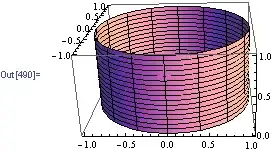
Dr. belisarius
- 115,881
- 13
- 203
- 453
-
Yet another possibility:
ParametricPlot3D[RotationTransform[θ, {0, 0, 1}][{1, 0, r}] // Evaluate, {r, 0, 1}, {θ, 0, 2 π}]– J. M.'s missing motivation Sep 17 '12 at 11:00 -