Using NIntegrate to integrate functions with sharp peaks (Lorentzian-like)

Question

I have a problem with NIntegrate that I do not understand. I want to integrate a function f[x], which has a complicated analytic expression, but appears as a sum of narrow Lorentzian peaks. The function is defined so that $0 \leq f(x) \leq 1$ for all $x$:

Plot[f[x], {x, -0.9, 0}, PlotRange -> All, PlotLabel -> "f[x]"]

If I now integrate the function numerically in the plotted interval, I get an unrealistically high result:

NIntegrate[f[x], {x, -0.9, 0}, Method -> "MonteCarlo"]

NIntegrate::maxp: The integral failed to converge after 50100 integrand evaluations. NIntegrate obtained 3.111064646506622`*^24 and 9.60509125990105`*^22 for the integral and error estimates. >>

3.11106*10^24

I tried to play around with different Nintegration methods, but the same order of magnitide shows up as a result. After some inspection, I found that the large contribution is located around $x= -0.81$. But here, $f(x)$ takes tiny values.

Does anyone know why I get this huge value? The same behavior of the function shows up when I use immediate definition:

g[x_] = f[x];
Plot[g[x], {x, -0.825, -0.8}, PlotPoints -> 150, PlotLabel -> "g[x]"]

Answer 1

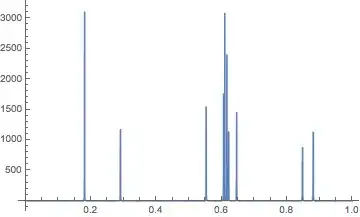
The NIntegrate behavior you observe over your integrand is described and explained in the section "Examples of Pathological Behavior" in the chapter "NIntegrate Integration Rules" of the Advanced NIntegrate documentation .

Using larger values for the options MinRecursion, MaxRecursion, and PrecisionGoal would probably fix your issue.

NIntegrate[f[x], {x, 0, 1}, PrecisionGoal -> 12, MinRecursion -> 12, 
 MaxRecursion -> 20]

Longer answer with code

The estimates and plot shown below illustrate how the overestimation can happen.

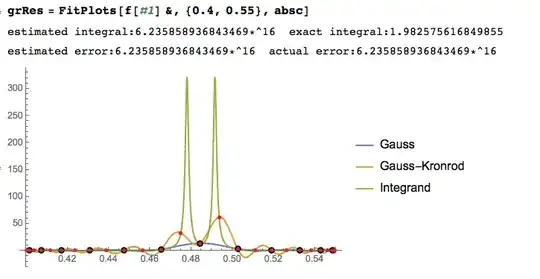
The plot shows the integrand and the polynomials corresponding to the abscissas and weights of the Gauss-Kronrod integration rule.

Below is the code for the image above. I used the code from the cited document and an integrand function generated in a fashion similar to that of the answer of Dr. belisarius.

Clear[f]
f[x_] := 318.31/(1 + 1.*^6*(-0.49158 + x)^2) + 
  318.31/(1 + 1.*^6*(-0.478 + x)^2)

Plot[f[x], {x, 0.3, 0.8}, PerformanceGoal -> "Quality", 
 PlotPoints -> 10000, PlotRange -> All]

{absc, weights, errweights} = 
  NIntegrate`GaussKronrodRuleData[12, MachinePrecision];

Clear[FitPlots];
FitPlots[f_, {a_, b_}, abscArg_] := 
  Module[{absc = 
     Rescale[abscArg, {0, 1}, {a, 
       b}]},(*this finds the interpolating polynomial through the \
Gauss abscissas and the values of f over them*)
   polyGauss[x_] := 
    Evaluate[
     InterpolatingPolynomial[
      Transpose[{Take[absc, {2, -2, 2}], 
        f[#1] & /@ (Take[absc, {2, -2, 2}])}], x]];
   (*this finds the interpolating polynomial through the Gauss-
   Kronrod abscissas and the values of f over them*)
   polyGaussKronrod[x_] := 
    Evaluate[
     InterpolatingPolynomial[Transpose[{absc, f[#1] & /@ absc}], x]];
   (*plot of the Gauss interpolating points*)
   samplPointsGauss = 
    Graphics[{GrayLevel[0], PointSize[0.02], 
      Point /@ 
       Transpose[{Take[absc, {2, -2, 2}], 
         f[#1] & /@ Take[absc, {2, -2, 2}]}]}];
   (*plot of the Gauss-Kronrod interpolating points*)
   samplPointsGaussKronrod = 
    Graphics[{Red, PointSize[0.012], 
      Point /@ Transpose[{absc, f[#1] & /@ absc}]}];
   (*interpolating polynomials and f plots*)

   Block[{$DisplayFunction = Identity},
    funcPlots = Plot[{
        Tooltip[polyGauss[x], "Gauss"],
        Tooltip[polyGaussKronrod[x], "Gauss-Kronrod"],
        Tooltip[f[x], "Integrand"]}, {x, a, b},
       PlotRange -> All, PerformanceGoal -> "Quality", 
       PlotPoints -> 10000, 
       PlotLegends -> {"Gauss", "Gauss-Kronrod", "Integrand"}];];
   exact = Integrate[f[x], {x, a, b}];
   r1 = Integrate[polyGauss[x], {x, a, b}];
   r2 = Integrate[polyGaussKronrod[x], {x, a, b}];
   Print["estimated integral:" <> ToString@InputForm@r2, 
    "  exact integral:" <> ToString@InputForm@Re@exact];
   Print["estimated error:" <> ToString@InputForm@Abs[r1 - r2], 
    "  actual error:" <> ToString@InputForm@Abs[r2 - exact]];
   Show[{funcPlots, samplPointsGauss, samplPointsGaussKronrod}]
   ];

grRes = FitPlots[f[#1] &, {0.4, 0.55}, absc]

Answer 2

You may try for example:

(* Lorentzians*)

f[x_] := Tr@Evaluate@Table[PDF[CauchyDistribution[a, .0001], x], 
                           {a, RandomReal[{.1, .9}, 10]}]

Plot[Evaluate@f[x], {x, 0, 1}, Filling -> Axis, PlotRange -> All]

NIntegrate[f[x], {x, 0, 1}, Method -> "LocalAdaptive"]
(* 9.99831 *) (*Quite good,should be 10 *)

Answer 3

Another possibility for integrating functions with wildly varying features is to avoid NIntegrate[] altogether, and consider reformulating as an initial value problem that can then be handled by NDSolve[]. Since DE solvers are often more careful than quadrature routines, they are less likely to miss sharp peaks or other features that usually give quadratures trouble.

Thus,

BlockRandom[SeedRandom[0]; (* bel's/Michael's example *)
            f[x_] = Sum[PDF[CauchyDistribution[a, .0001], x],
                        {a, RandomReal[{.1, .9}, 10]}]];

AbsoluteTiming[NDSolveValue[{y'[x] == f[x], y[0] == 0}, y[1], {x, 1, 1},
                            Method -> "Extrapolation"]]
   {0.118919, 9.998274818835679}

(Thanks to Michael for pointing out a more compact way to evaluate the resulting InterpolatingFunction[] at the terminal value.)

Answer 4

If the function is like that of @Dr. b., one might divide the interval up programmatically, to help NIntegrate find the important regions and still use a "GlobalAdaptive" strategy.

Dr. belisarius's Lorentzians:

(*Lorentzians*)
SeedRandom[0];               (* for reproducibility *)
f[x_] := Evaluate@Tr@
  Table[PDF[CauchyDistribution[a, .0001], x], {a, RandomReal[{.1, .9}, 10]}]        

Plot[Evaluate@f[x], {x, 0, 1}, Filling -> Axis, PlotRange -> All]

We divide the integration regions at the local maxima, up to a tolerance (10^-12 below, but it should depend on the interval of integration, as well as perhaps f). The function new tries to find a new maximum at a starting point, usually the midpoint between two maxima. The function subdivide subdivides the interval if there is a local maximum between the end points, provided the new maximum is significantly different from the end points (governed by the tolerance 1*^-12 in this case).

new = FindArgMax[f[x], {x, #}, Method -> {"Newton", "StepControl" -> "TrustRegion"}] &;

subdivide[{a_, b_}] := With[{c = First@new[(a + b)/2]},
  If[a + 1*^-12 < c < b - 1*^-12,
   {subdivide[{a, c}], subdivide[{c, b}]},
   {a, b}]
  ];

The integral evaluates without difficulty.

NIntegrate[
  f[x],
  {x,
   Sequence @@ Cases[subdivide[{0., 1.}], {a_Real, b_Real} :> a, Infinity],
   1.}] // AbsoluteTiming
(*  {0.30745, 9.99827}  *)

The division points, for the curious:

Cases[subdivide[{0., 1.}], {a_Real, b_Real} :> a, Infinity]
(* 
  {0., 0.180879, 0.290761, 0.553081, 0.606456, 0.61005,
   0.61642, 0.621974, 0.64625, 0.848162, 0.88095}
*)