murray wrote:
I've always had trouble getting the syntax of Through correct, since to me it seems more natural if it were instead Through[{Max, Min, Median, Mean}][y]
each[x : _[__]][arg__] := Through[ x @ arg ]
foo // each[bar[a, b, c]]
(* out: bar[a[foo], b[foo], c[foo]] *)
Sequence[foo, bar] // each[{a, b, c}]
(* out: {a[foo, bar], b[foo, bar], c[foo, bar]} *)
I rather like that idea. Thanks, murray.
Comments below Bob Hanlon's answer remind me one thing this lacks as written is the ability to work with held arguments, which #[y] & /@ {f1, f2, . . .} has by nature. If I am going to actually use this abstraction I will need to address that. One possibility:
ClearAll[each]
each[x : _[__]] := Function[, Through @ Unevaluated @ x[##], HoldAll]
Now:
2 + 2 // each[{Hold, HoldForm, Defer, MakeBoxes}]
(* out: {Hold[2 + 2], 2 + 2, 2 + 2, RowBox[{2, +, 2}]} *)
Update: also notably this case which is a bit harder to get with Map:
2 + 2 // each[ Hold[foo, bar, baz] ]
(* out: Hold[foo[2 + 2], bar[2 + 2], baz[2 + 2]] *)
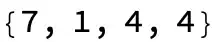

Through:Through[{Max, Min, Median, Mean}[y]]. – Leonid Shifrin Feb 18 '16 at 22:46