is there any way to use the Apply[] function to a sum of objects? By this I mean the following. We know that using Apply[] (@@) to an objects gives:
f@@{a}
f[a]
I'm wondering if there's a way of doing something like
(f+g)@@{a}
f[a]+g[a]
Does anyone knows anything about it? Thanks!
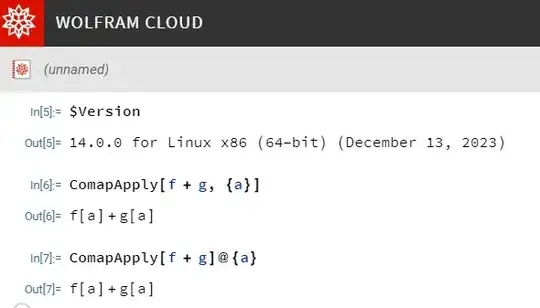
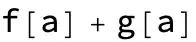
Through[Sequence@@@(f + g)@{a}]orThrough[(f + g)[a]]? (orSequence@@@(f + g)@{a}//Through) – user1066 Sep 24 '21 at 22:18#@a & /@ (f + g)– Bob Hanlon Sep 25 '21 at 02:34Through[(f + g)[a]]orThrough[(f + g) @@ {a}]– Ben Izd Sep 25 '21 at 07:38