Drawing circular patches around arbitrary points on a sphere

Question

I am trying to draw circular patches of given angular radii around arbitrary points on a sphere. I am able to use, for example,

SphericalPlot3D[1, {θ, 0, Pi/3}, {ϕ, 0, 2 Pi}, PlotStyle -> {Black, Opacity[0.7]}, 
                Mesh -> None]

and

SphericalPlot3D[1, {θ, (2 Pi)/3, Pi}, {ϕ, 0, 2 Pi}, PlotStyle -> {Black, Opacity[0.7]},
                Mesh -> None]

to create angular patches of (angular) radius $\pi/3$ around the north and south poles of the sphere, respectively, but what if I want to create two patches around two arbitrary points on the surface of the sphere, and then draw in the rest of the sphere in some other background color? Thank you!

score 6 · Answer 1 · answered Oct 12 '16 at 01:10

Here is a routine that renders a spherical cap on a unit sphere as a NURBS surface:

sphericalCap[{θ_, φ_}, α_] := With[{c = Cos[α/2]},
         Style[BSplineSurface[Map[RotationTransform[{{0, 0, 1}, 
                                  Append[{Cos[θ], Sin[θ]} Sin[φ], Cos[φ]]}], 
               Map[Function[pt, Append[#1 pt, #2]],
                   {{1, 0}, {1, 1}, {-1, 1}, {-1, 0}, {-1, -1}, {1, -1}, {1, 0}}] & @@@
                   {{0, 1}, {Sin[α/2]/c, 1}, {Sin[α], Cos[α]}}], 
               SplineClosed -> {False, True}, SplineDegree -> 2, 
               SplineKnots -> {{0, 0, 0, 1, 1, 1},
                               {0, 0, 0, 1/4, 1/2, 1/2, 3/4, 1, 1, 1}}, 
               SplineWeights -> Outer[Times, {1, c, 1}, {1, 1/2, 1/2, 1, 1/2, 1/2, 1}]], 
               BSplineSurface3DBoxOptions -> {Method -> {"SplinePoints" -> 25}}]]

Examples:

Graphics3D[{Opacity[0.7, Black], sphericalCap[{0, 0}, π/6]}, Axes -> True]

an inky cap

BlockRandom[SeedRandom["spherecaps"];
            Graphics3D[{EdgeForm[], Table[{Append[RandomColor[], 2/3], 
                        sphericalCap[{RandomReal[{0, 2 π}], RandomReal[{0, π}]}, 
                                     RandomReal[{0, π/4}]]}, {10}]}]]

various colored spherical caps

Graphics3D[{Directive[EdgeForm[], GrayLevel[1/5],
                      Glow[Blend[{Brown, Yellow}, 1/4]], Specularity[Gray, 25]], 
            sphericalCap[{ArcTan @@ Most[#], ArcCos[Last[#]]},
                         ArcCos[(80 + 9 Sqrt[5])/109]/2] & /@ 
            N[PolyhedronData["TruncatedIcosahedron", "VertexCoordinates"]/
              PolyhedronData["TruncatedIcosahedron", "Circumradius"]]}, 
           Boxed -> False, Lighting -> "Neutral"]

spherical caps on a truncated icosahedron

score 5 · Accepted Answer · edited Aug 19 '17 at 02:30

5

Show[
 SphericalPlot3D[1, {θ, 0, π}, {ϕ, 0, 2 π}, Mesh -> None,  RegionFunction -> 
        Function[{x, y, z, θ, ϕ, r}, Norm[{x, y, z} - {1, 1, 0}] > 1], PlotStyle -> Red], 
 SphericalPlot3D[1, {θ, 0, π}, {ϕ, 0, 2 π}, Mesh -> None, RegionFunction -> 
        Function[{x, y, z, θ, ϕ, r}, Norm[{x, y, z} - {1, 1, 0}] < 1], PlotStyle -> Blue]]

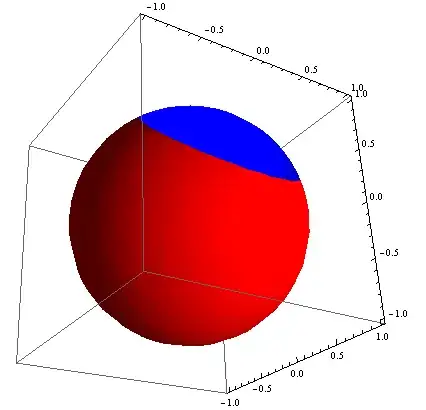
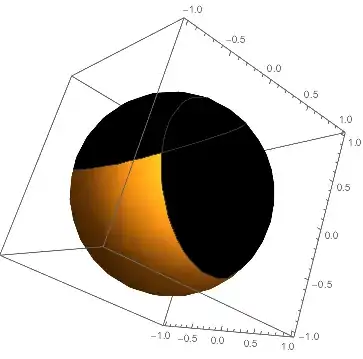
Mathematica graphics

edited Aug 19 '17 at 02:30

J. M.'s missing motivation

124,525
11
401
574

answered Feb 23 '16 at 00:05

Dr. belisarius

115,881
13
203
453

Thank you very much! I'm still digging into the specifics of RegionFunction and its implementation in your answer, but it seems as though I can control the radius of the circular patch by changing the inequality threshold value and the point about which the patch is centered by changing the constant vector ({1,1,0} in your example). – AnInquiringMind Feb 23 '16 at 00:26
@PhysicsCodingEnthusiast yep, that's it :) – Dr. belisarius Feb 23 '16 at 00:37
Just for future reference (this can be added into the answer above), Norm[{x,y,z}-{x1,y1,z1}] < c defines a ball of radius c centered at (x1,y1,z1). It is, to me, easier to define the center of the ball to be on the surface of the sphere, so (x1,y1,z1) = R(sin\theta cos\phi, sin\theta sin\phi, cos\theta). Then, to get a circular patch with angular radius \gamma centered at (\theta, \phi) (or, equivalently, (x1,y1,z1)), the radius of the ball (with center (x1,y1,z1)) should be c = R \sqrt{ 2(1 - cos\gamma) }. – AnInquiringMind Feb 23 '16 at 04:00

score 5 · Answer 3 · answered Feb 23 '16 at 00:38

Here's a way using MeshFunctions and MeshShading that generalized to any number of points.

pts = Normalize /@ RandomReal[{-1, 1}, {2, 3}];
angles = Table[{Pi/3}, Length@pts];
SphericalPlot3D[1, {θ, 0, Pi}, {ϕ, 0, 2 Pi}, 
 MeshFunctions -> 
  Table[With[{v0 = v0}, 
    Function[{x, y, z, θ, ϕ}, 
     VectorAngle[{x, y, z}, v0]]], {v0, pts}],
 Mesh -> angles,
 MeshShading -> {{Black, Black}, {Black, Automatic}},
 BoundaryStyle -> None]

Mathematica graphics

More random points, random angles:

SeedRandom[7];
pts = Normalize /@ RandomReal[{-1, 1}, {3, 3}];
angles = RandomReal[0.66, {Length@pts, 1}];
shading = ReplacePart[
   ConstantArray[Black, Table[2, Length@pts]], 
   Table[-1, Length@pts] -> Automatic];
SphericalPlot3D[1, {θ, 0, Pi}, {ϕ, 0, 2 Pi},
 PlotPoints -> 50, 
 MeshFunctions -> 
  Table[With[{v0 = v0}, 
    Function[{x, y, z, θ, ϕ}, 
     VectorAngle[{x, y, z}, v0]]], {v0, pts}],
 Mesh -> angles,
 MeshShading -> shading,
 BoundaryStyle -> None, MeshStyle -> None]

Mathematica graphics

Thank you for your answer! I had already accepted the first answer, as it worked for my purposes, but I definitely appreciate you taking the time to answer my question! — AnInquiringMind, Feb 23 '16 at 04:10
@PhysicsCodingEnthusiast You're welcome! Sometimes you'll find people giving advice to wait 24 hours before accepting an answer. Not having an accepted answer encourages other to take a look to see if they can do better. Also, since our active users are found all around the world, which is really cool, imo, some may not get a chance to view your question until well after you've posted it. But feel free to accept whichever answer you think is best whenever you want. — Michael E2, Feb 23 '16 at 14:08

Drawing circular patches around arbitrary points on a sphere

3 Answers3

Linked