Is there a way to randomly distribute points within a circle on the surface of a sphere?

Question

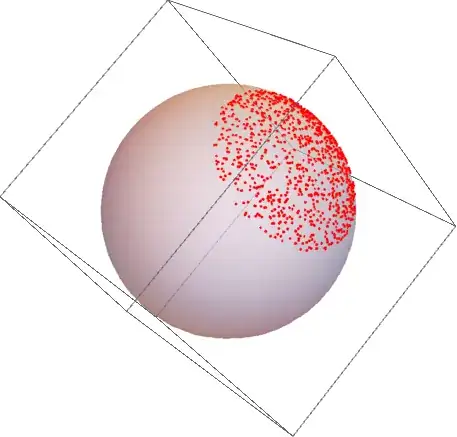
I'm attempting to set up a situation where on a 3D sphere, I choose a random point and construct a circle around this point with some radius. I then want to randomly distribute points within this circle. Is there a straightforward way to do this?

I have no trouble finding random points on the surface of the sphere; however I cannot seem to find a way to distribute points randomly on a closed region of the sphere.

Many thanks for any help in advance.

You could brute force it by finding random points on the sphere, then throwing away any that aren't inside the desired region. — Foo Bar, Nov 18 '19 at 12:59
@Foo, yes, one can certainly use the rejection method for this. The tricky part is in figuring out how not to throw away too many points. — J. M.'s missing motivation, Nov 18 '19 at 14:37
Depends on your underlying distribution. I assume you want uniform random over the sphere's area. For contrast, consider uniform random points in a circle and then project the circle onto the sphere. That's still random but with a different distribution function. — Carl Witthoft, Nov 19 '19 at 19:39

score 19 · Answer 1 · answered Nov 18 '19 at 04:13

19

You can intersect the sphere and a cylinder, and then use RandomPoint. For example, here is a random point on the sphere:

sphere = Sphere[];
SeedRandom[1]
pt = RandomPoint[sphere]

{0.707037, 0.595614, 0.381239}

Then, you create a cylinder in he direction of the random point with a radius:

r = .7;
cylinder = Cylinder[{{0,0,0},pt}, r];

Now, intersect the cylinder and the sphere and use RandomPoint:

reg = RegionIntersection[cylinder, sphere];
pts = RandomPoint[reg, 1000];

Visualization:

Graphics3D[{Sphere[], Red, Point @ pts}]

answered Nov 18 '19 at 04:13

Carl Woll

130,679
6
243
355

1

Can you verify that this produces uniform random per unit sphere area (as opposed to some projection of the intersecting circle)? I"m not familiar with how this Mathematica function actually selects points. – Carl Witthoft Nov 19 '19 at 19:41
1

@CarlWitthoft That's what the documentation says: "RandomPoint will generate points uniformly in the region reg." In this case the region is the spherical cap. – Carl Woll Nov 19 '19 at 20:36

score 11 · Answer 2 · answered Nov 18 '19 at 05:08

Using Christian Blatter's results from this math.SE answer, here is how to randomly sample a spherical cap:

randomCapPoint[{r_, r2_}, dir_?VectorQ] := With[{h = RandomReal[{Sqrt[1 - (r2/r)^2], 1}]}, 
      RotationTransform[{{0, 0, 1}, Normalize[dir]}][r
      Append[Sqrt[1 - h^2] Normalize[RandomVariate[NormalDistribution[], 2]], h]]]

For example,

BlockRandom[SeedRandom[1337]; (* for reproducibility *)
            With[{r = 1, r2 = 2/5, d = {1.3, -2.4, 2}, n = 5000}, 
                 Graphics3D[{{Opacity[1/2], Sphere[{0, 0, 0}, r]},
                             {Blue, Arrow[Tube[{{0, 0, 0}, Normalize[d]}]]},
                             {Directive[AbsolutePointSize[2], Orange], 
                              Point[Table[randomCapPoint[{r, r2}, d], {n}]]}}]]]

random points on spherical cap

Same question as at Carl Woll's answer: how do you verify the spatial distribution is "uniform" with respect to sphere area? — Carl Witthoft, Nov 19 '19 at 19:43
@Carl, using the results in Christian's answer, you could take a histogram of the longitude and colatitude of the sample points, and verify that they have the required distribution. — J. M.'s missing motivation, Nov 19 '19 at 20:51

score 8 · Answer 3 · answered Nov 18 '19 at 06:51

We can also take RandomPoints in boolean region obtained by the RegionIntersection of a Sphere and a Ball with radius r centered at a random point on the sphere:

SeedRandom[1]
r = .7;

ctr = RandomPoint[Sphere[]];

pts = RandomPoint[RegionIntersection[Ball[ctr, r], Sphere[]], 1000];

Graphics3D[{Red, Point@pts, White, Opacity[.5], Sphere[]}]

score 1 · Answer 4 · answered Nov 19 '19 at 19:52

1

You can use Archimedes' result (https://en.wikipedia.org/wiki/On_the_Sphere_and_Cylinder) that the area between two lines of latitude is the same as the corresponding area of the enclosing cylinder.

This gives a fairly simple result for sampling the top of the sphere, above height Z

pt[Z_] := Module[{z, θ, r},
  z = RandomVariate[UniformDistribution[{Z, 1}]];
  θ = RandomVariate[UniformDistribution[{0, 2 π}]];
  r = Sqrt[1 - z^2];
  {r Cos[θ], r Sin[θ], z}]

answered Nov 19 '19 at 19:52

mikado

16,741
2
20
54

This is basically what my method does, except I replaced {r Cos[θ], r Sin[θ]} with r Normalize[RandomVariate[NormalDistribution[], 2]]. – J. M.'s missing motivation Nov 19 '19 at 20:49

Is there a way to randomly distribute points within a circle on the surface of a sphere?

4 Answers4

Linked