Restrict a curve to an intersection with another one

Question

Code

p=0.5; r=0.1; x1=100; x2=10; x3=7;
Ec12R[N_] := x1 - x2 (1 + 2 N) + 2 (1 + N) N (1/p - 1) (1 + r)
Ec13R[N_] := x1 - x3 (1 + 2 N) + 2 (1 + N) N (1/p - 1) (1 + r)
Ed12R[N_] := x1 - x2
Es13R[N_] := Es13R[N_] := x1 - (1 + 2 N (1 + N))/(2 (1 + 2 N)) (x2 + x3) + (2 N^2 (1+r) (1/p - 1))/(1 + 2 N)
Plot[{Ed12R[N], Es13R[N], Ec13R[N], Ec12R[N]},
  {N, 1, 15},
  AxesLabel -> {"N", "E"},
  BaseStyle -> {FontSize -> 12},
  PlotRange -> {0, 100},
  AxesOrigin -> {1, 0},
  Ticks -> None
 ]

How can I restrict the yellow (Ec13R[N]) and green (Ec12R[N]) curve in a way that they do not continue after they intersect with red (Es13R[N])? So I want to remove any value (of yellow and green) to the right of the intersection with red in the graph.

Please post your actual Mathematica code. Without it no one will be able to see what you might have done wrong, nor will they be able to experiment with possible repairs. — m_goldberg, Mar 03 '16 at 09:46
not very general, but for starters, Plot[{x, If[x^2 - 5 < x, x^2 - 5, Unevaluated@Sequence[]]}, {x, 0, 8}] — LLlAMnYP, Mar 03 '16 at 10:00
Plot[Sin[x], {x, 0, 8 Pi}, RegionFunction -> Function[{x, y}, Abs[y] > 0.5]] — tsuresuregusa, Mar 03 '16 at 12:25
See How do I plot a function over a subset of the displayed interval? — , Mar 03 '16 at 14:18
@NiklasK. Please see your edited post for how to correctly format code blocks. In addition, N is reserved symbol in Mathematica. In general, it is a good idea not to use capitalized symbol names, since all built-in Mathematica functions begin with capital letters. — march, Mar 03 '16 at 17:11
Defining anything with a capital letter in the beginning is begging for trouble. N, E and I have very specific meanings in Mma, and you might collide with a predefined name with mysterious results even on longer names. N happens to work in this case for very specific reasons, but you couldn't use it as a normal variable, for instance... — kirma, Mar 03 '16 at 18:36

score 3 · Accepted Answer · edited Apr 13 '17 at 12:55

You can use ConditionalExpression, which returns Undefined if the condition doesn't hold. Plot understands this, and doesn't try to plot anything on undefined values.

p = 0.5; r = 0.1; x1 = 100; x2 = 10; x3 = 7;
Ec12R[x_] := x1 - x2 (1 + 2 x) + 2 (1 + x) x (1/p - 1) (1 + r);
Ec13R[x_] := x1 - x3 (1 + 2 x) + 2 (1 + x) x (1/p - 1) (1 + r);
Ed12R[x_] := x1 - x2;
Es13R[x_] := 
  x1 - (1 + 2 x (1 + x))/(2 (1 + 2 x)) (x2 + 
      x3) + (2 x^2 (1 + r) (1/p - 1))/(1 + 2 x);

onlyBelow[eqn_, limit_] := ConditionalExpression[eqn, eqn < limit];

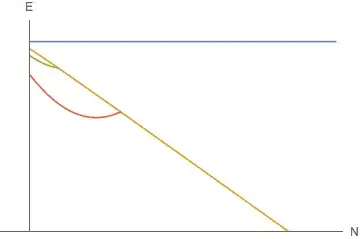
Plot[{Ed12R[x], Es13R[x], onlyBelow[Ec13R[x], Es13R[x]], 
  onlyBelow[Ec12R[x], Es13R[x]]}, {x, 1, 15}, AxesLabel -> {"N", "E"},
  BaseStyle -> {FontSize -> 12}, PlotRange -> {0, 100}, 
 AxesOrigin -> {1, 0}, Ticks -> None]

Arbitrarily complicated constraints can be constructed if necessary. For instance:

beforeNextCrossing[f1_, limitf_, var_, firstval_] := 
  ConditionalExpression[f1[var], 
   var < Module[{x}, 
     Min[x /. Quiet@Solve[{f1[x] == limitf[x], x > firstval}, x]]]];

Plot[{Ed12R[x], Es13R[x], beforeNextCrossing[Ec13R, Es13R, x, 1], 
  beforeNextCrossing[Ec12R, Es13R, x, 1]}, {x, 1, 15}, 
 Evaluated -> True, AxesLabel -> {"N", "E"}, 
 BaseStyle -> {FontSize -> 12}, PlotRange -> {0, 100}, 
 AxesOrigin -> {1, 0}, Ticks -> None]

This produces the same result, but actually computes where the next crossing of plots occurs on x larger than 1. (Note that I added Evaluated -> True option. It forces beforeNextCrossing to be evaluated before plotting, instead of on every value of x.)

EDIT:

I want to refer to my recent answer (How to find the next root larger than a specified value, numerically?) featuring findNextRoot for a bit more robust method of finding a specific crossing like this. Using it, beforeNextCrossing can be written as:

beforeNextCrossing[f1_, limitf_, var_, firstval_] := 
 ConditionalExpression[f1[var], 
  var < (var /. First@findNextRoot[f1[var] == limitf[var], {var, firstval}])]

Restrict a curve to an intersection with another one

1 Answers1