1

A similar question has been asked in the post HERE but the current question is more complicated: I have the following differential system

XX = x'[t] == x[t] (1 - x[t]) (1 - Exp[-0.4 y[t]] - 0.2);
YY = y'[t] == 0.4 (-0.5 y[t]^0.2 + (1 - x[t])) ;

SOL = NDSolve[{XX, YY, x[0] == 18/100, y[0] == 40/100}, {x,y}, {t, 0, 100}]

The solution of this differential system yields the interpolating functions

{{x->InterpolatingFunction[{{0.`,100.`}},"<>"],y->InterpolatingFunction[{{0.`,100.`}},"<>"]}}

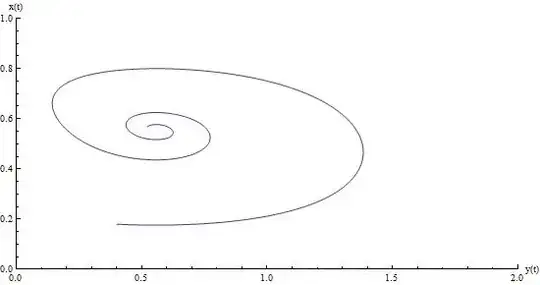
I know that for some $y$'s there are multiple $x$'s because the dynamical relationship is non-linear, see the picture below 

x[t_] = Evaluate[x[t] /. SOL[[1]]]
y[t_] = Evaluate[y[t] /. SOL[[1]]]
ParametricPlot[{y[t], x[t]}, {t, 0, time}, AxesLabel -> {"y(t)", "x(t)"}, PlotRange -> {{0, 2}, {0, 1}}]

enter image description here

My question is: how can I extract, for a given level of $y$, the (potentially) multiple solutions of $x$ and the $t$ at which this occurs?

The importance is that the interpolation function is a function of two variables which are itself functions of time, and that I want to find all multiple solutions for $x$ for a given $y$. (The previous question HERE has only one argument in the interpolation function and it only yields unique solutions.)

Thank you sincerely for your help.

Community
  • 1
user2085
  • 91
  • 5
  • 1
    Without the full code that generated the interpolating function, can't say for sure. But you could try NSolve to get the t values and then plug them into the x function. – Jason B. Mar 24 '16 at 14:51
  • 2
    If it's an option, it might be easier to use WhenEvent to get the values you're looking for right in the NDSolve. – Chris K Mar 24 '16 at 15:12
  • 1
    You can use WhenEvent[] for this (if it's a one-time deal), or the MeshFunctions option of Plot[]/ParametricPlot[] in conjunction with FindRoot[]. There are a lot of previous threads on how to use these to find intersection points. – J. M.'s missing motivation Mar 31 '16 at 00:09
  • Part 1: A simple solution is to solve e.g. the interpolation function $y[t]$ for $t$ at a specific value of $y[t]$ via FindRoot (NSolve does not seem to work, it yields an InverseFunction solution and not an explicit solution). Finding the different roots can be done using THIS or THIS – user2085 Apr 03 '16 at 07:33
  • 1
    Part 2: or THIS approach. Then one can substitute the different $t$'s into the interpolating function for $x[t]$ and has the sets of solutions. – user2085 Apr 03 '16 at 07:37

0 Answers0