I would like to put a dot on the point of a curve that has a specific y value but I don't know the x value.
A simple example of my code is
eqns = {y''[t] + y[t] == 3 a Sin[y[t]], y[0] == y'[0] == 1};
pfun = ParametricNDSolveValue[eqns, y[1] + y[2], {t, 0, 5}, {a}];
Plot[pfun[a], {a, -2, 2}]
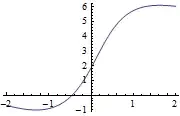
So say I want to find the x at which y=3. How? Once I have the two coordinates I know how to add the dot. I guess I'm confused because the interpolating function gives you the y given the x, and I can't figure out how to do the inverse. Also any suggestions of tutorials on how to use interpolating functions would be great. Thanks!
xandy. – Daniel Lichtblau Jun 11 '13 at 00:01