3

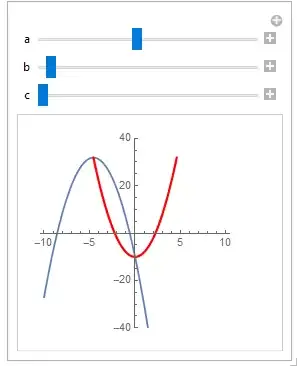
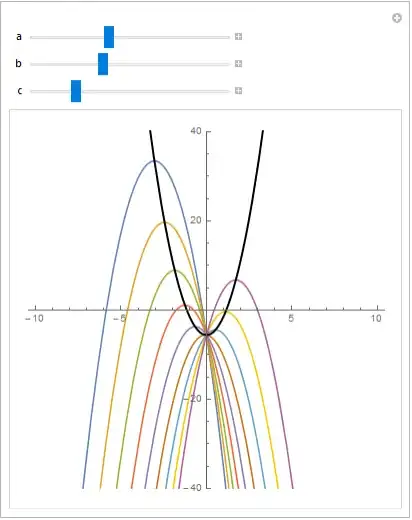
For the parabola y = a x^2+ b x + c I want to see the locus of the vertex as b varies (with a and c to be parameters). What are the ways to plot the locus of the parabola dynamically in Mathematica?

I am very new to Mathematica, so I could figure out only basic Manipulate:

Manipulate[
  Plot[a x^2 + b x + c, {x, -10, 10}, PlotRange -> 40, AspectRatio -> 1], 
   {a, -20, 20}, {b, -20, 20}, {c, -10, 10}
 ]

I would like to see the locus parabola appearing in the same manner as in the post, if possible.

Thanks.

Community
  • 1
Lokesh Jaddu
  • 33
  • 3
  • Can you give more details about exactly what you want? As it is, this is likely to be closed as being unclear what you're asking. – march Mar 25 '16 at 17:43
  • 1
    I want something like this. A animation where the locus of the vertex of the parabola is plotted as i manipulate a,b,c. – Lokesh Jaddu Mar 26 '16 at 01:59

1 Answers1

3
Manipulate[
 plot1 = Plot[a x^2 + b x + c, {x, -10, 10}, PlotRange -> 40, 
   AspectRatio -> 1, ImageSize -> Small];
 plot3 = If[a == 0, Graphics[], 
   ParametricPlot[{-u / (2 a), a (-u / (2 a))^2 + u (-u / (2 a)) + c}, {u, -b, b}, 
    PlotStyle -> {Red, Thick}]];

 Show[plot1, plot3],

 {{a, -2}, -20, 20}, {b, -20, 20}, {c, -10, 10}, 
 TrackedSymbols :> True]

enter image description here

Edit Another method to visualize locus:

Manipulate[
  f[x_, i_] := a x^2 + (b + i) x + c;
  tmp = Table[f[x, i], {i, -20, 20, 5}];

  plot1 = Plot[tmp, {x, -10, 10}, PlotRange -> 40, AspectRatio -> 1];
  plot2 = Plot[Tooltip[-a x^2 + c, "Locus"], {x, -10, 10}, PlotStyle -> {Black, Thick}];

  Show[plot1, plot2],

{a, -20, 20}, {b, -20, 20}, {c, -10, 10}, TrackedSymbols :> True]

enter image description here

Edit2 Note on connection between first and second parts. Notice in 'plot3' we have used parametric form.

Solve[{x == -b / (2 a), y == a x^2 + b x + c}, {x, y}] // FullSimplify

$y=c-\frac{b^2}{4 a}$ and $x^2=\frac{b^2}{4 a^2}$.

So, we may come back from parametric to cartesian equation $y= - a x^2 + c$

(this equation is used in plot2).

garej
  • 4,865
  • 2
  • 19
  • 42