3

I have been having tremendous success with my students due to the following idea:

expandLog = {Log[x_] + Log[y_] :> Log[x y], n_ Log[x_] :> Log[x^n]}

collectLog = {Log[x_ y_] :> Log[x] + Log[y], Log[x_^n_] :> n Log[x]}

Written on Simplify expressions with Log by RunnyKine. Extremely easy to understand and to explain to the students. However, I've finally encountered a difficulty:

This worked:

enter image description here

But this didn't:

enter image description here

I tried a number of different things, like using the Algebraic Manipulation Palette, highlighting the interior, but none worked.

Any suggestions?

Community
  • 1
David
  • 14,883
  • 4
  • 44
  • 117

1 Answers1

4

You just need to write a general rule that takes a base like this:

logbaserule = {Log[k_, x_] + Log[k_, y_] :> Log[k, x y], n_ Log[k_, x_] :> Log[k, x^n]};

revlogbaserule = {Log[k_, x_ y_] :> Log[k, x] + Log[k, y], Log[k_, x_^n_] :> n Log[k, x]};

Now you can apply to your question:

Log[2, x + Sqrt[x^2 - 1]] + Log[2, x - Sqrt[x^2 - 1]] //. logbaserule // Simplify

0

You can also use FullSimplify with a transformation function to go directly to the final result:

tf[x_] := x /. logbaserule

FullSimplify[Log[2, x + Sqrt[x^2 - 1]] + Log[2, x - Sqrt[x^2 - 1]], 
                 TransformationFunctions -> {Automatic, tf}]

0

RunnyKine
  • 33,088
  • 3
  • 109
  • 176
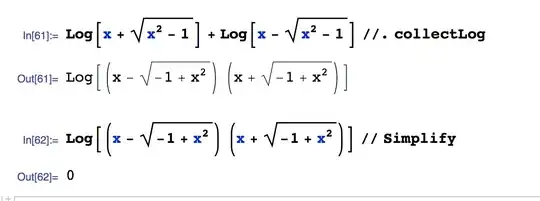
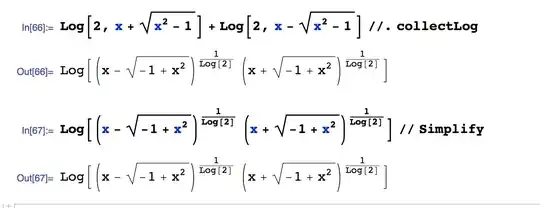
  • It is nice as the approach, but why the result is zero? Evaluation Log[2, x + Sqrt[x^2 + 1]] + Log[2, x - Sqrt[x^2 + 1]]/.x->0 yields (I \[Pi])/Log[2], rather than zero. – Alexei Boulbitch Mar 29 '16 at 07:42
  • No, I substituted x->0 above. I mean that the approach is, in principle good, but the answer is wrong. On my machine the application of logbaserule gave me a correct answer, but FullSimplify gave 0. – Alexei Boulbitch Mar 29 '16 at 08:36
  • @AlexeiBoulbitch What do you get when you multiply x + Sqrt[x^2 - 1] by x - Sqrt[x^2 - 1] and Simplify? If you get 1, then Log of 1 should be 0 – RunnyKine Mar 29 '16 at 08:43
  • @RunnyKine Thanks for your response. This is quite helpful for my students. – David Mar 29 '16 at 16:41
  • @David. You're welcome, glad I could help. – RunnyKine Mar 29 '16 at 16:51