Let us introduce the function to transform the logarithm:
collectLog[expr_] := Module[{rule1, rule2, a, b, x},
rule1 = Log[a_] + Log[b_] -> Log[a*b];
rule2 = x_*Log[a_] -> Log[a^x];
(expr /. rule1) /. rule2 /. rule1 /. rule2
];
This is your expression:
expr = (n Log[a] + m Log[b] - m Log[a + b] - n Log[a + b]);
Let us first simplify it, and then apply to it the collectLog function:
expr2 = Simplify[expr, {a > 0, b > 0},
TransformationFunctions -> {Automatic, ComplexExpand}] //
collectLog
The result is
Log[a^n b^m] + Log[(a + b)^(-m - n)]
Let us apply the collectLog once more:
expr2 // collectLog
The result is:
Log[a^n b^m (a + b)^(-m - n)]
Done.
To answer the recent question of bszd: if a function with multiple Logs may be designed.
It can be done in a more simple way. If one has a lengthily expression with logarithms of the sort that might be simplified by collection, the function Nest may do the job:
Nest[collectLog, expr, Length[expr]]
The answer is:
Log[a^n b^m (a + b)^(-m - n)]
If it is only a part of expression that, however, contains multiple logarithms to be collected, the function
collectAllLog[expr_] := Nest[collectLog, expr, Length[expr]];
may be mapped onto this part.
Finally, to complete this one may need to do the opposite operation: to expand the logarithmic expression. One way to do this would be to use the following function:
expandLog[expr_] := Module[{rule1, rule2, a, b, x},
rule1 = Log[a_*b_] -> Log[a] + Log[b];
rule2 = Log[a_^x_] -> x*Log[a];
(expr /. rule1) /. rule2
];
and
expandAllLog[expr_] := Nest[expandLog, expr, Depth[expr]]
For example,
expandAllLog[Log[a^n b^m (a + b)^(-m - n)]]
yields
n Log[a] + m Log[b] + (-m - n) Log[a + b]
as expected.
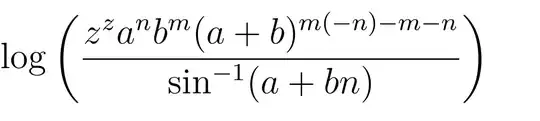
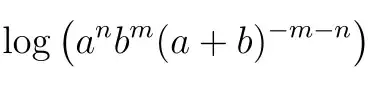
Assuming[{n > 0, m > 0, a > 0, b > 0}, FullSimplify[n Log[a] + m Log[b] == Log[a^n b^m]]]is True. So, these assumptions should be sufficient, but I cannot let it make the simplification itself. – Sjoerd C. de Vries Apr 04 '13 at 22:23PowerExpand[]. – loki Dec 14 '17 at 13:40