Extracting unknown ColorFunction from Plot, Plot3D etc

Question

I wonder if there is a way to extract existing ColorFunction and "override" it with a new function that will depend on original one. This question discusses different ways how to add transparency to 3D plot, including an "extraction procedure" proposed by @RunnyKine:

Trace[Plot[Sin[x], {x, 0, 2 Pi}], _Blend & ] // 
  Flatten // ReleaseHold
Trace[Plot[Sin[x], {x, 0, 2 Pi}, 
    ColorFunction -> "Rainbow"], _Blend &] // Flatten // ReleaseHold
Trace[Plot[Sin[x], {x, 0, 2 Pi}, 
    ColorFunction -> (#^2 &)], _Blend &] // Flatten // ReleaseHold

It works if you know in advance that the ColorFunction uses Blend, but for general ColorFunction (case three in the above code) it doesn't work. These were just examples to illustrate the extraction algorithm. I want a procedure that will work for any plotting object without any assumptions about its ColorFunction.

Is there a way to obtain ColorFunction from plotting functions? I wonder if I'm missing some simple solution a la

ColorFunction /. Options[Plot] (* Automatic .. not very useful *)

Answer 1

This doesn't allow the extraction and reconstruction of the unknown ColorFunction, but it does allow to override it with an exact duplicate that is transparent,

plt1 = Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> (#^2 &),
    ImageSize -> 300];
plt2 = Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> (Hue[#^2] &), 
   ImageSize -> 300];
plt3 = Plot[Sin[x], {x, 0, 2 Pi}, 
   ColorFunction -> (LABColor[#^2, #, 1 - #] &), ImageSize -> 300];
{plt1, plt2, plt3}
{plt1, plt2, plt3} /. a_ /; ColorQ[a] :> Directive[Opacity[.5], a]

Edit

So extracting a color function from a plot is not simple, and I haven't got a one-size fits all solution. Basically, you need to extract the colors from the plot, extract the points, order the colors and the points together, and then use Blend to create a color interpolating function.

To top it off, the original plot may have used x or y to base their color function on. Here's an example, where I use a ColorFunction which is just a modified form of one of the built-in.

reconstructColorFunction[plt2_] := 
 Module[{order, points, colors, reconstructedcolorfunc1, 
   reconstructedcolorfunc2},
  order = Cases[plt2, Line[{a__}, b__] :> a, Infinity];
  points = 
   Cases[plt2, GraphicsComplex[{a__}, b__] :> a, Infinity][[order]];
  colors = (Cases[plt2, Rule[VertexColors, {a__}] :> a, 
       Infinity] /. {a_?(SameQ[ArrayDepth[#], 2] &) :> (RGBColor /@ 
          a), a_?(SameQ[ArrayDepth[#], 1] &) :> (GrayLevel /@ 
          a)})[[order]];
  reconstructedcolorfunc1 = 
   Blend[Transpose[{points[[All, 1]], colors}], #] &;
  reconstructedcolorfunc2 = 
   Blend[Transpose[{points[[All, 2]], colors}], #] &;
  {BarLegend[{reconstructedcolorfunc1[#] &, 
     MinMax@points[[All, 1]]}],
   BarLegend[{reconstructedcolorfunc2[#] &, 
     MinMax@points[[All, 2]]}]}
  ]

Here it is tested on a few built-in color functions

{plot1, plot2, plot3, 
  plot4} = {Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> (#2^2 &), 
   ImageSize -> 300],
  Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> (#1^2 &), 
   ImageSize -> 300],
  Plot[Sin[x], {x, 0, 2 Pi}, 
   ColorFunction -> (ColorData["BlueGreenYellow"][#2^2] &), 
   ImageSize -> 300],
  Plot[Sin[x], {x, 0, 2 Pi}, 
   ColorFunction -> (ColorData["BlueGreenYellow"][#1^2] &), 
   ImageSize -> 300]}

reconstructColorFunction /@ {plot1, plot2, plot3, plot4}

Answer 2

I don't think it's possible to extract such information from an already evaluated plot. Plot returns a Graphics object and very little meta-information is stored. We can see this by inspecting with InputForm.

InputForm[Plot[1, {x, 0, 1}, ColorFunction -> Hue, PlotPoints -> 2]]

Graphics[{GraphicsComplex[{{1.*^-6, 1.}, {0.999999, 1.}, {0.5, 1.}}, 
 {{{}, {}, {Directive[Opacity[1.], RGBColor[0.368417, 0.506779, 0.709798], AbsoluteThickness[1.6]], Line[{1, 3, 2}, VertexColors -> Automatic]}}}, 
 VertexColors -> {Hue[0.], Hue[0.], Hue[0.]}], {}}, {DisplayFunction -> Identity, PlotRangePadding -> {{Scaled[0.02], Scaled[0.02]}, {Scaled[0.05], Scaled[0.05]}}, 
 PlotRangeClipping -> True, ImagePadding -> All, DisplayFunction -> Identity, AspectRatio -> GoldenRatio^(-1), Axes -> {True, True}, AxesLabel -> {None, None}, 
 AxesOrigin -> {0, 0}, DisplayFunction :> Identity, Frame -> {{False, False}, {False, False}}, FrameLabel -> {{None, None}, {None, None}}, 
 FrameTicks -> {{Automatic, Automatic}, {Automatic, Automatic}}, GridLines -> {None, None}, GridLinesStyle -> Directive[GrayLevel[0.5, 0.4]], 
 Method -> {"DefaultBoundaryStyle" -> Automatic, "DefaultMeshStyle" -> AbsolutePointSize[6], "ScalingFunctions" -> None}, PlotRange -> {{0, 1}, {0., 2.}}, 
 PlotRangeClipping -> True, PlotRangePadding -> {{Automatic, Automatic}, {Automatic, Automatic}}, Ticks -> {Automatic, Automatic}}]

But we can somewhat reverse engineer the ColorFunction and approximate it with interpolating functions.

First here's a plot with a custom ColorFunction:

plot = Plot[Sin[Pi x], {x, -1, 1}, 
  ColorFunction -> (ColorData["FruitPunchColors", Max[-#1, #2]] &)]

Now extract the data points and the color information. Note colors are either stored as an array or as explicit colors, so we need to check for both. Also if there was no ColorFunction to begin with, this method will fail, though one could modify the code to account for that case.

pts = First[Cases[plot, GraphicsComplex[l_, ___] :> l, Infinity]];
colors = First[Join[
  Cases[plot, _[VertexColors, l_?ArrayQ] :> l, Infinity],
  Cases[plot, _[VertexColors, l:{__?ColorQ}] :> List @@@ ColorConvert[l, "RGB"], Infinity]
]];

Now interpolate.

{red, green, blue} = 
  Interpolation[Transpose[{pts, #}], InterpolationOrder -> 1] & /@ Transpose[colors];

Now here's where it gets a bit hand-wavy. Our data is not of full measure, so extrapolation will need to be used. It seems like restricting the domain to the convex hull of our data gives reasonable results though.

dom = ConvexHullMesh[pts];
Show[dom, plot]

And now sample values only in this domain. They look reasonable to me.

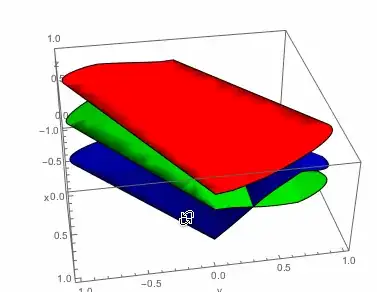
Plot3D[
  {red[x, y], green[x, y], blue[x, y]}, 
  {x, y} ∈ dom, 
  AxesLabel -> {"x", "y", "z"}, 
  Mesh -> None, 
  PlotStyle -> {Red, Green, Blue}
]

I'm not sure if I've really addressed your question. So please ask if you'd like me to elaborate on something.

Answer 3

It looks like the original method was copied from my answer to The default ColorFunction of DensityPlot before v10? That was not intended to be a universal reusable function, only an expedient interactive way to get the information desired.

Neither that original case nor as I perceive them the examples in your own question require the recovery of a color function from an already evaluated Plot as JasonB and Chip Hurst attempted; that is surely a far harder problem! I think instead you "merely" need to find what the color function either is defined by or will resolve to for an unevaluated Plot expression.

It is easy enough to extract an explicitly specified ColorFunction, or one specified with SetOptions, using a replacement rule and OptionValue.* However this does not easily find values set through the Plot Theme or resolve Automatic into an actual color function. The Theme case could be handled as done in How to access new colour schemes in version 10? or Match colors to plot themes but one will find that that sometimes resolves to Automatic, and it turns out we can handle both using one method so I propose skipping PlotTheme resolution.

For this we can use Trace as we started with but we need to make it more general. A bit of spelunking indicates that we can intercept Legend information to do this.

Attributes[getLegendData] = HoldFirst;

getLegendData[expr_, key_String] :=
  Flatten[
    Trace[expr, System`ProtoPlotDump`legendData @ key, TraceForward -> True]
  ][[2, 1]]

Testing:

p[1] := Plot[Sin[x], {x, 0, 2 Pi}];
p[2] := Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> "Rainbow"];
p[3] := Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> (#^2 &)];
p[4] := DensityPlot[x y, {x, y} ∈ Disk[], PlotTheme -> "Classic"]
p[5] := DensityPlot[x y, {x, y} ∈ Disk[]]

getLegendData[p[#], "ColorFunction"] & ~Array~ 5 // Column

• Note that the second argument is a String, "ColorFunction".

• Strings that appear in this Trace are known to include

  {"ArgumentExpression", "ArgumentLength", "AspectRatio", "AutoLegend", "BarOrigin", 
  "BaseStyle", "BoundaryStyle", "ChartBaseStyle", "ChartElements", "ChartLayout", 
  "ChartStyle", "ColorFunction", "ColorFunctionScaling", "Contours", "DataExtremes", 
  "DefaultLabels", "DefaultLegendFunction", "DefaultOptions", "Depth", "Dimensions", 
  "ImageSize", "Joined", "LabelStyle", "LegendAppearance", "PlotMarkers", 
  "PlotStyle", "StyleWrappers", "WrapperLegends"}
  

---

* Since Trace involves evaluation of the Plot we may sometimes want the simpler but less robust method. Here is a generalized function to complement setOpts from Setting options of expressions similar to using SetOptions on objects:

Attributes[getOpts] = HoldFirst;

getOpts[p : h_[___], option_] :=
  Unevaluated[p] /.
    HoldPattern[h][___, OptionsPattern[]] :>
      OptionValue[option]

Now:

getOpts[Plot[Sin[x], {x, 0, 2 Pi}], ColorFunction]

getOpts[Plot[Sin[x], {x, 0, 2 Pi}, ColorFunction -> (#^2 &)], ColorFunction]

getOpts[Grid[{}, Background -> Red], {Alignment, Frame, Background}]

Automatic
#1^2 &
{{Center, Baseline}, None, RGBColor[1, 0, 0]}