11

Bug introduced in 7.0 or earlier and fixed in 11.0

This is a follow-up to this question regarding numerical instabilities occurring with modified Bessel functions. In trying to explore J.M.'s answer to that question in greater depth by setting WorkingPrecision -> 50 (as advised in the other answer by xslittlegrass), I obtained vastly different (and incorrect!) results than when not explicitly setting a non-default WorkingPrecision (see below for plots). I am trying to figure out why this is occurring and was advised to make a separate question regarding this.

The function that I am attempting to plot (for fixed $b$, as a function of $a$) is

f[a_, b_] := (a^2 Exp[a^2/(8 b)] (BesselK[3/4, a^2/(8 b)] - 
  BesselK[1/4, a^2/(8 b)]))/(8 Sqrt[a b^3])

which is the analytic solution to

Integrate[x^2 Exp[-a x^2 - b x^4], {x, -∞, ∞}, Assumptions -> {a > 0, b > 0}]

I also plot the numerical solution to this,

g[a_,b_] := NIntegrate[x^2 Exp[-a x^2 - b x^4], {x, -∞, ∞}]

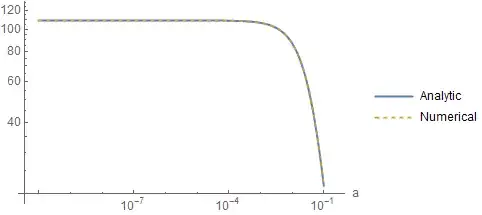
Without any regards to WorkingPrecision, I obtain the following plot:

amin = 10^-10; amax = 0.1; bval = 10^-3;
LogLogPlot[{f[a, bval], g[a, bval]}, {a, amin, amax}, PlotRange -> All]

enter image description here

Even with explicitly giving the variable/bounds higher precision,

amin = 1`50 10^-10; amax = 0.1`50; bval = 1`50 10^-3;

the plot remains the same as above. If, however, I add in WorkingPrecision -> 50, a plot with function values many orders of magnitude higher is obtained:

amin = 1`50 10^-10; amax = 0.1`50; bval = 1`50 10^-3;
LogLogPlot[{f[a, bval], g[a, bval]}, {a, amin, amax}, WorkingPrecision -> 50,
             PlotRange -> All]

enter image description here

The fact that this is occurring is worrisome, as I would generally expect the results obtained with higher WorkingPrecision to be more trustworthy; in this case, however, they are completely wrong -- here's a representative plot:

bval = 10^-3;
Plot[x^2 Exp[-a x^2 - bval x^4] /. a -> 10^-5, {x, -15, 15}]

enter image description here

Why is this happening? Thank you very much!

Community
  • 1
AnInquiringMind
  • 743
  • 3
  • 11

1 Answers1

12

There appears to be a bug, not in Integrate or in BesselK, but in the vertical-axis Ticks of LogLogPlot. Consider the simple case,

LogLogPlot[Exp[x], {x, 10^-10, 1}, PlotRange -> All]

enter image description here

as it should be. However,

LogLogPlot[Exp[x], {x, 10^-10, 1}, WorkingPrecision -> 50, PlotRange -> All]

enter image description here

In fact, any value of WorkingPrecision except MachinePrecision triggers this error. Even WorkingPrecision -> $MachinePrecision produces the error.

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
  • Oh my. That would be quite unfortunate. I will have to see if this issue arises for various functions when I'm at my computer again tomorrow morning – this is something that would somehow need to be reported to the appropriate Wolfram team, right? – AnInquiringMind May 24 '16 at 04:40
  • @PhysicsCodingEnthusiast Absolutely. Will you do so, or do you wish me to? Your call. – bbgodfrey May 24 '16 at 04:41
  • I can do so – is there a good way to do this? Should I provide a link to this question? I'll wait to do it until I'm at my computer again (currently on my phone) – in the meantime, perhaps others will chime in with their own findings. Thanks! – AnInquiringMind May 24 '16 at 04:44
  • @Physics, yes, please do link to this question as evidence if and when you make a report. – J. M.'s missing motivation May 24 '16 at 04:50
  • @PhysicsCodingEnthusiast Report the bug here. Do not be surprised, if the response is slow. – bbgodfrey May 24 '16 at 04:54
  • @PhysicsCodingEnthusiast The response is usually not slow. But the developers do seem to take their time in fixing certain bugs. – QuantumDot May 24 '16 at 18:19