Bug introduced in 7.0 or earlier and fixed in 11.0.0
(I'm using Mathematica 8.)
I have a Taylor series:
poly = Normal[Series[E^x, {x, 0, 10}]]
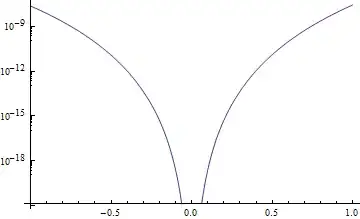
I want to produce a log-linear plot of the error. This is easy enough with the following code:
LogPlot[Abs[E^x - poly], {x, -1, 1}]
This produces
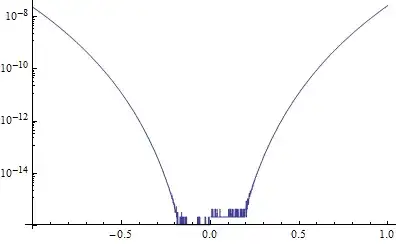
Now, I want to plot even smaller values of the error (in particular I want the plot to be sensible near zero), so I tell LogPlot to use high precision as follows:
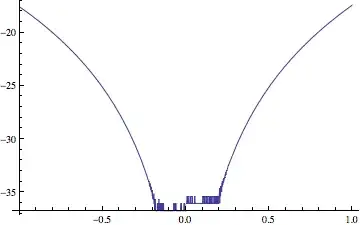
LogPlot[Abs[E^x - poly], {x, -1, 1}, WorkingPrecision -> 30]
However this destroys the labeling on the y-axis:
![bad behavior of LogPlot[]](../../images/912eb5d74408084a3f4b85a1f09d1cdf.webp)
Does anyone know what has gone wrong here? How do I fix it?
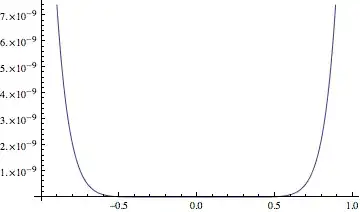


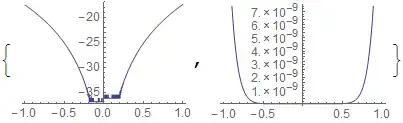


WorkingPrecision -> MachinePrecisionwill use machine precision (default).WorkingPrecision -> $MachinePrecisionwill not use machine precision, but the built-in arbitrary precision with the same number of digits as machine precision. For high precision you would not wantMachinePrecision, but set a higher number inWorkingPrecision(which as you noticed produces a plot with a wrong scale). – Szabolcs Dec 03 '12 at 17:26WorkingPrecision, as in your example, crashes version 9. Can anyone reproduce this in 9? – Szabolcs Dec 03 '12 at 17:27Plotto adaptively increase the working precision (by up to$MaxExtraPrecisionbase-10 digits) in order to produce an accurate plot, whereas without precision tracking it has no way to know when numerical errors become significant." ... Anyway to avoid confusion I've just set theWorkingPrecisionto 30 in the question. – AUK1939 Dec 03 '12 at 17:38