ListPlot of data with small differences

Question

This following is a similar question as plot data with small differences, but I am not able to solve my problem with the proposed solutions.

list = {1.00000012, 1.00000012, 1.00000013, 1.00000014, 1.00000015};

All of the commands produce the same non-scaled plot:

ListPlot[list, PlotRange -> All]
ListPlot[list, PlotRange -> Full]
ListPlot[list, PlotRange -> Automatic]

All commands above produce the same non-scaled plot:

Your syntax is just a bit off. The PlotRange specs has to be PlotRange -> {{xmin, xmax}, {ymin, ymax}}, where one or both {min,max} can be Automatic. So you can do ListPlot[list, PlotRange -> {Automatic, {Min[list], Max[list]}}] — Marius Ladegård Meyer, Jun 01 '16 at 14:17
Or, if you're using 10.1 and higher, use MinMax, e.g. PlotRange -> {Automatic, MinMax[list]}. — rcollyer, Jun 01 '16 at 18:00
@chuy: how would you solve this with Standardize, that looks promising. — mrz, Jun 01 '16 at 21:50
ListPlot[Standardize[list], PlotRange-> All,Frame-> True, Axes-> False, Filling-> Axis] is one possible way. The y-axis now represents how many standard deviations a point is away from the mean. — chuy, Jun 02 '16 at 13:53

score 5 · Accepted Answer · edited Apr 13 '17 at 12:55

5

Using the solution provided by Mr.Wizard in this answer:

list = {1.00000012, 1.00000012, 1.00000013, 1.00000014, 1.00000015};

ListPlot[list, "AllowMicroRanges" -> True]

To get useful yticks, one can use for example

ListPlot[list, "AllowMicroRanges" -> True, 
 Ticks -> {Automatic, N[FindDivisions[{#1, #2}, 7], 10] &}]

edited Apr 13 '17 at 12:55

Community

1

answered Jun 01 '16 at 20:01

Karsten7

27,448
5
73
134

2

Great ... the 5th point is only wrong ... to be honest the documentation of mathematica is sometimes very short, incomplete and this undocumented functions, methods, etc. are annoying ... I would like to know from Wolfram what the strategy behind that is? – mrz Jun 02 '16 at 09:30
Yes it works excellent without any additional adjustments (v. 10.4.1). – mrz Jun 03 '16 at 08:20

score 4 · Answer 2 · answered Jun 01 '16 at 17:44

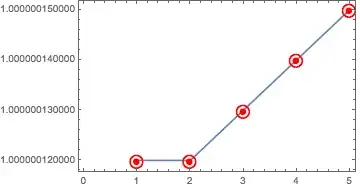
Here is an approach that essentially sidesteps whatever problem ListPlot seems to have in creating an appropriate plot range and ticks. Instead of plotting the values themselves, it may be more useful to plot the differences between the values and the minimum to highlight a trend. The rest of the code is just there to create some reasonably readable ticks, expressed in "parts per billion difference" on the vertical axis:

ListPlot[
 list - Min[list],
 PlotStyle -> {Red, PointSize[0.02]},
 PlotRange -> {{0.5, 5.5}, Automatic},
 PlotRangePadding -> {None, Scaled[0.1]},
 Frame -> True, Axes -> None,
 FrameLabel -> {None, Style["difference / ppb", Black, 16]},
 FrameTicks ->
  {Automatic,
   Function[{min, max},
    With[{vals = Subdivide[0, Round[max, 1*^-8], 6]},
     Transpose@
      {vals, Rationalize[1*^9 vals, 0]}
    ]
   ]
  },
 FrameTicksStyle -> Directive[Black, 12]
]

final plot

As an aside, this is an example of the kind of gymnastics that are sometimes necessary to produce a decent-looking plot in MMA, and a strong case for the use of e.g. SciDraw, which makes some of these adjustments quite a bit more flexible.

You can simplify the task by plotting 10^9 (list - Min[list]) — Bob Hanlon, Jun 01 '16 at 18:12
@BobHanlon Very true. When that first didn't occur to me, I decided to muck with the ticks, and developed tunnel vision... Thanks for the suggestion! — MarcoB, Jun 01 '16 at 19:08
@MarcoB: This is sometimes of advantage what you propose to plot the differences. I was in general interested why ListPlot has no method to do it on its own (see the AllowMicroRanges Option in the solution of Karsten 7. who got it from Mr.Wizard). — mrz, Jun 02 '16 at 09:35

score 3 · Answer 3 · answered Jun 01 '16 at 15:08

3

I'll propose ListLogPlot because;

list = {1.00000012, 1.00000012, 1.00000013, 1.00000014, 1.00000015}

{1., 1., 1., 1., 1.}

myList = SetPrecision[list, 9]

{1.00000012, 1.00000012, 1.00000013, 1.00000014, 1.00000015}

ListLogPlot[{myList}, Frame -> True, Joined -> True, 
PlotMarkers -> Style["⦿", Large, Red]]

As an alternative you can use ScalingFunctions

ListPlot[myList, ScalingFunctions -> "Log", Frame -> True]

answered Jun 01 '16 at 15:08

This helps ... it is strange why for the linear scaling plot there seems not to be a solution which sets the best vertical plot range. – mrz Jun 01 '16 at 16:26

ListPlot of data with small differences

3 Answers3