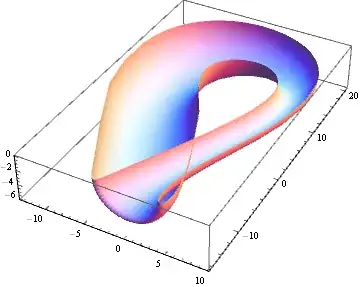
I have found the following parametrisation for a Klein bottle:
a = 6 Cos[2 u] (1 + Sin[u]);
b = 16 Sin[u];
c = 4 (1 - Cos[u]/2);
fx = If[Pi < u <= 0, a + c Cos[v + Pi], a + c Cos[u] Cos[v]];
fy = If[Pi < u < 2 Pi, b, b + c Sin[u] ];
fz = c Sin[v];
I am trying to plot it using
ParametricPlot3D[{fx, fy, fz}, {u, 0, 2 Pi}, {v, 0, 2 Pi},
Boxed -> False, Axes -> False]
but the result is not quite the Klein bottle.
The reference I am using is this one (page 141) where you can see the same parameterization.
- Any ideas why it does not work with me?
- Also how can I change the colours of the surface to be as in the book?




PlotTheme -> "Classic". – Yves Klett Jun 21 '16 at 09:24ExampleData[{"Geometry3D", "KleinBottle"}]– Greg Hurst Jun 21 '16 at 16:36