18

I came across this post while messying around the StackExchange mobile. I think this thing can be easily done by Mathematica as well but I'm not an expert in geometric field. Can anyone give some solutions?

This problem is open to all kinds of answers at all times!

desired image

related link that may help when creating points: click me click me~

Community
  • 1
Wjx
  • 9,558
  • 1
  • 34
  • 70

3 Answers3

36

This is probably too slow to get a decent image, but here's a simple attempt. As JM suggests, you can use Geodesate to get a good set of points on the sphere. I used ContourPlot3D to plot a sphere whose radius increases in the vicinity of one of those points.

Needs["PolyhedronOperations`"]

pts = Geodesate[PolyhedronData["Icosahedron"], 2][[1, 1, 14 ;;]];

nf = Nearest[N@pts];

f[x_?NumericQ, y_, z_] :=
 With[{d = Normalize[{x, y, z}] - First[nf[{x, y, z}]]},
  1 + 0.5 Exp[-300 (d.d)]]

ContourPlot3D[x^2 + y^2 + z^2 == f[x, y, z], 
  {x, -1.2, 1.2}, {y, -1.2, 1.2}, {z, -1.2, 1.2}, Mesh -> None, ContourStyle -> Green]

enter image description here

The surface has some holes, and obviously there are not enough spikes (increase the geodesation order to get more). You can fiddle with the lighting and surface specularity to make it look more shiny.

update

It is faster to use SphericalPlot3D of course:

pts = Geodesate[PolyhedronData["Icosahedron"], 4][[1, 1, 14 ;;]];
nf = Nearest[N@pts];
f[x_?NumericQ, y_, z_] := With[{d = Normalize[{x, y, z}] - First[nf[{x, y, z}]]}, 
  1 + 0.25 Exp[-300 (d.d)]]
g[θ_, ϕ_] := f[Sin[θ] Cos[ϕ], Sin[θ] Sin[ϕ], Cos[θ]]

SphericalPlot3D[g[θ, ϕ], {θ, 0, Pi}, {ϕ, 0, 2 Pi}, 
 PlotPoints -> 100, Mesh -> None, 
 PlotStyle -> Directive[Darker@Green, Specularity[White, 30]], 
 Lighting -> "Neutral", Background -> Black, Boxed -> False, Axes -> False]

enter image description here

Simon Woods
  • 84,945
  • 8
  • 175
  • 324
  • I was momentarily confused, but then realized your convention for $\theta$ and $\varphi$ is opposite to mine. :D – J. M.'s missing motivation Jun 25 '16 at 14:27
  • It's wierd that I cannot do the same plotting with my data......How can I solve this problem? my data can be get via visiting the link I've posted. If you can explain this, I will have no hesitation to select your question. :) Thanks! – Wjx Jun 25 '16 at 14:55
  • @Wjx, I'm not sure what the problem is. With pts = Normalize /@ pt my visualisation works fine with your points? – Simon Woods Jun 25 '16 at 15:11
  • oops, sorry, my fault that I didn't normalize that before using it. Silly mistake. :P thank you verrrry much! – Wjx Jun 25 '16 at 15:13
  • 2
    (+1) Instead of using PolyhedronOperations`Geodesate, you could do pts = MeshCoordinates[DiscretizeGraphics[Sphere[], MaxCellMeasure -> .01]]; and get very similar results. – Greg Hurst Oct 07 '16 at 20:35
20

A mathematical approach using $A_\text{g}$ irreps of $I_h$ symmetry group expressed in terms of spherical harmonics. First some data

l[1] = 6;
mlist[1] = {-5, 0, 5};
slist[1] = {Sqrt[7]/5, Sqrt[11]/5, -(Sqrt[7]/5)};

l[2] = 10;
mlist[2] = {-10, -5, 0, 5, 10};
slist[2] = {Sqrt[187/3]/25, -(Sqrt[209]/25), Sqrt[247/3]/25, Sqrt[
   209]/25, Sqrt[187/3]/25};

l[3] = 12;
mlist[3] = {-10, -5, 0, 5, 10};
slist[3] = {Sqrt[741/5]/25, Sqrt[286/5]/25, (3 Sqrt[119/5])/
   25, -(Sqrt[(286/5)]/25), Sqrt[741/5]/25};

l[4] = 16;
mlist[4] = {-15, -10, -5, 0, 5, 10, 15};
slist[4] = {Sqrt[34017/5]/
   250, -(Sqrt[(84847/30)]/125), -(Sqrt[6851]/250), (4 Sqrt[589/3])/
   125, Sqrt[6851]/
   250, -(Sqrt[(84847/30)]/125), -(Sqrt[(34017/5)]/250)};

l[5] = 18;
mlist[5] = {-15, -10, -5, 0, 5, 10, 15};
slist[5] = {Sqrt[17081/5]/125, Sqrt[4389/5]/125, (6 Sqrt[38])/125, 
   Sqrt[4301]/125, -((6 Sqrt[38])/125), Sqrt[4389/5]/
   125, -(Sqrt[(17081/5)]/125)};

l[6] = 20;
mlist[6] = {-20, -15, -10, -5, 0, 5, 10, 15, 20};
slist[6] = {Sqrt[164021/5]/625, -((2 Sqrt[12958/5])/625), (
   41 Sqrt[323/5])/625, -(Sqrt[(206074/5)]/625), Sqrt[4669]/625, Sqrt[
   206074/5]/625, (41 Sqrt[323/5])/625, (2 Sqrt[12958/5])/625, Sqrt[
   164021/5]/625};

Now the actual computation

Do[ySAF[h, \[Theta]_, \[Phi]_] = 
   ComplexExpand[
     Re@Dot[slist[h], 
       SphericalHarmonicY[l[h], mlist[h], \[Theta], \[Phi]]]] // 
    Simplify;
 , {h, 1, 6}]

and plotting

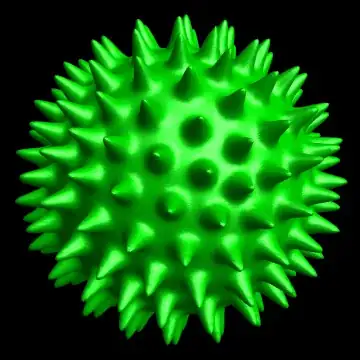
g = Table[SphericalPlot3D[(3 + ySAF[h, a, b]), {a, 0, \[Pi]}, {b, 0, 2 \[Pi]},
    PlotPoints -> 30, Mesh -> None, Axes -> False, 
   ColorFunction -> (ColorData["BlueGreenYellow"][1 - #6] &)], {h, 1, 6}]

with the following result

enter image description here

yarchik
  • 18,202
  • 2
  • 28
  • 66
  • 1
    I upvoted it because it's beautiful, but it is not quite spikey~ – Wjx Jun 25 '16 at 13:27
  • @Wjx I know, I hope someone here can apply some transformations to these functions to make them more spiky, have little time to do that. I do not mind though if it is posted as a separate answer – yarchik Jun 25 '16 at 13:32
  • Maybe for completeness, you can show how to generate the irreducible representations of the $I_h$ group from scratch. :) – J. M.'s missing motivation Jun 25 '16 at 14:29
  • @J.M. It is not very hard. One can start for instance with L=6 (this irrep can be generated using usual group theory approach). Then for not very high angular momentum other irreps can be extracted from the products. For instance, $6\times6 = 10+12$, $12\times12=16+18+20+22+24$, and so on. At L=30 there are more than 1 Ag, and the things get complicated... – yarchik Jun 25 '16 at 16:35
7
test = points[70];

With somewhat equally spaced points on the sphere from this answer.

Graphics3D[{Sphere[],
  test /. r : {x_, y_, z_} :> Cone[{.95 r, 1.25 r}, .1]},
 ImageSize -> Medium,
 Boxed -> False]

enter image description here

Community
  • 1
BoLe
  • 5,819
  • 15
  • 33