How to generate a Coronavirus 3D geometric model?

Question

How to generate a Coronavirus 3D geometric model like this one:

https://urbanmilwaukee.com/wp-content/uploads/2020/02/1024px3D_medical_animation_coronavirus_structure-1024x576.jpg

Or this one:

https://img-new.cgtrader.com/items/2300416/cbf78a951d/coronavirus-covid-19-3d-model-obj-fbx-ma-3b.jpg

Attempt

Here is some related code:

Block[{ang = -0.9`, dia = 0.04`, ext = 2.4`, turn = 20, r = 0.42}, 
 spring = ParametricPlot3D[
     r*{(ext + Cos[(2 turn x)/(1 - ang)]) Cos[x], 
       Sin[(2 turn x)/(
        1 - ang)], (ext + Cos[(2 turn x)/(1 - ang)]) Sin[x]}, {x, 
      0, (1 - ang) \[Pi]}, 
     PlotStyle -> {Lighter[Yellow], Tube[dia]}][[1, 1]];
 ]

shell = RegionPlot3D[
    2 <= x^2 + y^2 + z^2 <= 3 && (y > -0.5), {x, -2, 2}, {y, -2, 
     2}, {z, -2, 2}, PlotStyle -> Red, Mesh -> None, 
    PlotPoints -> 100, PlotTheme -> "Minimal"][[1, 1]];

Graphics3D[{shell, spring}, Boxed -> False, Background -> Black]

For the spiral formulas I used the code from this demonstration by Sandor Kabai: "Helical Spring between Two Cylinders".

Answer 1

UPDATE

I recommend taking a look at the following post:

3D Modeling of the SARS-CoV-2 Virus in the Wolfram Language https://community.wolfram.com/groups/-/m/t/1989540

ORIGINAL

One can also try to import 3D parts created by other people. If you search online you can probably find some sites. For instance, from here

https://3dprint.nih.gov/discover/coronavirus

you can get a model and combine it with your spiral (a bit resized):

obj=Import["https://wolfr.am/LNm1PWwN"];
spring=Block[{ang=-0.9`,dia=1,ext=2.4,turn=20,r=10},
ParametricPlot3D[r{
(ext+Cos[(2 turn x)/(1-ang)]) Cos[x],
Sin[(2 turn x)/(1-ang)]+.5,
(ext+Cos[(2 turn x)/(1-ang)]) Sin[x]},
{x,0,(1-ang) [Pi]},PlotStyle->{Lighter[Yellow],Tube[dia]}]];
Show[{obj,spring},PlotRange->{{-50,50},{-10,50},{-50,50}},ImageSize->400{1,1}]

Answer 2

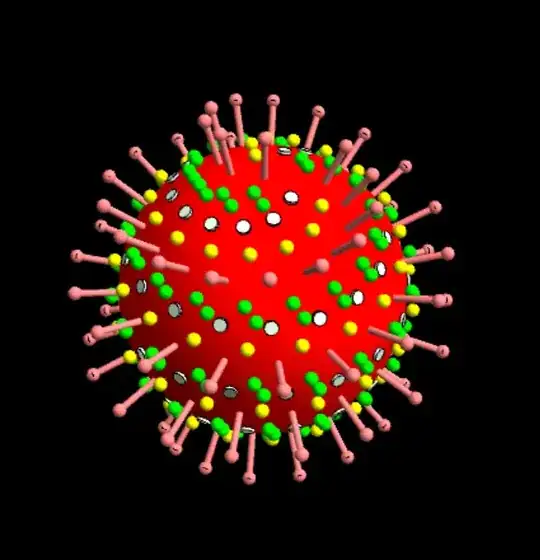
The problem of arranging four kinds of elements without intersection on a sphere has many solutions. I will indicate one of them. First, we will depict the entire sphere assuming that the elements are equally and their total number is 300:

p = SpherePoints[300];
p2 = Table[p[[2 i]], {i, 150}];
p1 = Table[p[[2 i - 1]], {i, 150}];
pS = Table[p2[[2 i]], {i, 75}]; pM = Table[p1[[2 i]], {i, 75}]; pE = 
 Table[p1[[2 i - 1]], {i, 75}];
pHE = Table[p2[[2 i - 1]], {i, 75}];
r1 = Sqrt[3]; r0 = Sqrt[2]; r2 = 
 r0 + 2.7 (Sqrt[3] - Sqrt[2]); dr = 0.04;

cylS = Table[{Pink, Cylinder[{r0 pS[[i]], r2 pS[[i]]}, dr]}, {i, 
    Length[pS]}];
sphS = {Pink, Sphere[r2 pS, 2 dr]};
cylE = Table[{Yellow, Cylinder[{r0 pE[[i]], r1 pE[[i]]}, dr/2]}, {i, 
    Length[pE]}];
sphE = {Yellow, Sphere[(r1 + 2 dr) pE, 2 dr]}; sphM = {Green, 
  Sphere[(r1 + 2 dr) pM, 2 dr]}; sphM1 = 
 Rotate[sphM, 5 dr/r1, {1, 1, 1}]; cylHE = 
 Table[{LightBlue, Cylinder[{r0 pHE[[i]], r1 pHE[[i]]}, dr]}, {i, 
   Length[pHE]}];
cylHEt = Table[{LightGreen, 
    Cylinder[{r1 pHE[[i]], (r1 + dr) pHE[[i]]}, 2 dr]}, {i, 
    Length[pHE]}];

Graphics3D[{{Red, Sphere[{0, 0, 0}, r1]}, cylS, sphS, cylE, sphE, 
  cylHE, cylHEt, sphM, sphM1}, Boxed -> False, Background -> Black, 
 Lighting -> "Neutral"]

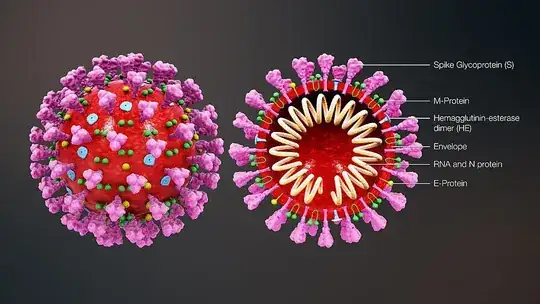
Cross section with RNA and penetrating elements:

Block[{ang = -0.9`, dia = 0.04`, ext =2.4`, turn = 20, r = 0.42}, 
 spring = ParametricPlot3D[
     r*{(ext + Cos[(2 turn x)/(1 - ang)]) Cos[x], 
       Sin[(2 turn x)/(1 - ang)], (ext + 
          Cos[(2 turn x)/(1 - ang)]) Sin[x]}, {x, 0, (1 - ang) \[Pi]},
      PlotStyle -> {Lighter[Yellow], Tube[dia]}][[1, 1]];]

shell = RegionPlot3D[
    r0^2 <= x^2 + y^2 + z^2 <= r1^2 && (y > -0.5), {x, -2, 2}, {y, -2,
      2}, {z, -2, 2}, PlotStyle -> Red, Mesh -> None, 
    PlotPoints -> 100, PlotTheme -> "Minimal"][[1, 1]];

{Graphics3D[{shell, spring, cylS, sphS, cylE, sphE, cylHE, cylHEt, 
   sphM, sphM1}, Boxed -> False, Background -> Black, 
  PlotRange -> {All, {-.0, 2}, All}], 
 Graphics3D[{shell, spring, cylS, sphS, cylE, sphE, cylHE, cylHEt, 
   sphM, sphM1}, Boxed -> False, Background -> Black, 
  PlotRange -> {All, {-.5, 2}, All}]}