I am interested in determining the minimum and maximum values of the real roots of polynomials of form $P(x)=\sum_{k=0}^n a_{k} x^k$ where $n$ will have a defined value (say 3,4,5...) and $a_k$ are chosen from the set $\{-1,1\}$ with equal probability.
I have tried creating a table of the roots, and then using MinMax; here is my (bad) attempt (with $n=3$):
T = Table[Roots[Sum[RandomChoice[{-1, 1}] x^k, {k, 0, 3}] == 0, x], 25]
MinMax[T]
Unfortunately, Roots gives both the real and imaginary roots, I would only like the real roots . Also, MinMax cannot work on the table $T$ when the roots are not presented as a list (they have $||$ in between each root).
Any suggestions/help with this issue is immensely appreciated. Thank You!
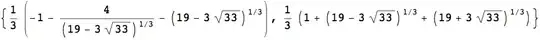
FindRoot, see a related problem First positive root – Artes Jun 28 '16 at 19:15