First positive root

Question

Simple question but problem with NSolve.

I need help how to extract first positive root?
For example:

 eq = -70.5 + 450.33 x^2 - 25 x^4;
 NSolve[ eq == 0, x]

If I have an equation eq that I am not sure of polynomial order and I need to define all positive roots x[1], ..., x[2].

Artes · Accepted Answer · 2012-12-19T19:21:21.400

The most straightforward way would be FindRoot[ eq, {x, 0}] but since this specific polynomial eq has a singular Jacobian at x == 0 (evaluate e.g. Reduce[ D[ eq, x] == 0, x]) one would rather use FindRoot[ eq, {x, x0}] for small x0 > 0. The argument x0 depends on a case by case basis, but for the problem at hand an appropriate value might be 0 < x0 <= 2.4, e.g. :

FindRoot[ eq, {x, 0.5}]

{x -> 0.397412}

More general considerations must include huge order polynomials, which might have many real roots. So finding every root may be very inefficient. In such cases there is a handy function RootInterval which can be much more efficient than any NSolve approach and especially handy when using it together with FindRoot.

First @ RootIntervals[eq]

{{-(273/64), -(263/64)}, {-(33/64), -(23/64)}, {47/128, 57/128}, {263/64, 273/64}}

It shows where one can find the first positive root , i.e. in this interval : {47/128, 57/128}. To choose only intervals where positive roots may be found we use e.g. :

intervals = First @ RootIntervals[eq] ~ DeleteCases ~ {_, _?Negative}

{{47/128, 57/128}, {263/64, 273/64}}

Then we use it for finding roots numerically with Brent's method -- the most powerful algorithm available for FindRoot :

roots = FindRoot[ eq, {x, #[[1]], #[[2]]}, Method -> "Brent"][[All, 2]]& /@ intervals //
        Flatten

{0.397412, 4.22555}

The last step is standard :

Min @ roots

0.397412

The first root might be negative therefore we could use e.g. :

RankedMin[roots, #]& /@ {1, 2}

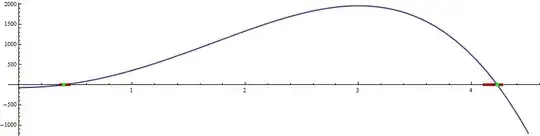
Now for the sake of completeness we demonstrate small intervals and roots on the plot of the polynomial over the positive reals :

Plot[ eq, {x, -4.5, 4.5}, PlotStyle -> Thick, AspectRatio -> 1/3, Epilog -> {
          Darker @ Red, Thickness[0.005], Line[{{#1, 0}, {#2, 0}}]& @@@ intervals,
          Green, PointSize[0.007], Point[{#, 0}] & /@ roots } ]

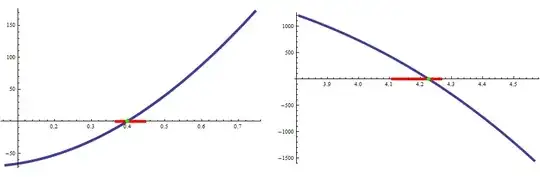
enter image description here

the same plot in pieces :

GraphicsRow[ 
    Plot[   eq, {x, #1 - 0.3, #2 + 0.3}, PlotStyle -> Thickness[0.01], Epilog -> {
                 Red, Thickness[0.011], Line[{{#1, 0}, {#2, 0}}] & @@@ intervals, 
                 Green, PointSize[0.015], Point[{#, 0}] & /@ roots}] & @@@ intervals ]

enter image description here

@Artes: How can you generalize your Code given above to a system of nonlinear equations? I am struggling to find real solutions to the NL system. Can you give me an example, for example, for a system of 5 nonlinear (NL) equations? and find the equilibrium limited to only real values. — Tugrul Temel, Apr 19 '19 at 10:25
@TugrulTemel eq==0 is a nonlinear equation, to solve a system you should use something like FindRoot[{eq1==0,...,eq5==0},{{x1,y0},...,{x5,y5}}] possibly with an appropriate method. For a specific problem you should better ask another question. Sometimes you can get solutions with Solve or NSolve with domain specification, eg. NSolve[{eq1==0,...eq5==0},{x1,...,x5},Reals]. — Artes, Apr 19 '19 at 15:32
@Artes: Thank you very much. I cannot figure out why NSolve is very slow for a system of 30 equations (mixed: linear and nonlinear). Regards. — Tugrul Temel, Apr 19 '19 at 18:37
@TugrulTemel It is not surprising, that solving systems of 30 equations is very slow. In such a case more reasonable is to exploit FindRoot. — Artes, Apr 19 '19 at 19:23

score 14 · Answer 2 · answered Dec 18 '12 at 21:29

14

    eq = -70.5 + 450.33 x^2 - 25 x^4;
    roots = x /. NSolve[eq == 0, x]
    Min@Select[roots, Positive]
0.397412

answered Dec 18 '12 at 21:29

murray

11,888
2
26
50

yes, but how to extract second, third ... separately? – Pipe Dec 18 '12 at 21:35
@Pipe you can use Sort instead of Min to get the ordered positive roots – ssch Dec 18 '12 at 21:35
@Nasser it is working but how to extract just second for example – Pipe Dec 18 '12 at 21:39
@Nasser Thank you very much, it is clear now – Pipe Dec 18 '12 at 23:14
1

@Pipe: Had you asked for how to extract the 2nd or 3rd, etc., I would have indeed have used Sort instead of Min. But you asked just for the 1st! – murray Dec 20 '12 at 15:54

score 5 · Answer 3 · edited Dec 19 '12 at 17:10

5

Well, if you wanted to give NSolve your conditions directly, you can do

NSolve[-70.5 + 450.33 x^2 - 25 x^4 == 0 && x > 0, x]

And then if you want, you can pick the Min solution.

edited Dec 19 '12 at 17:10

Artes

57,212
12
157
245

answered Dec 19 '12 at 15:09

cartonn

1,005
6
15

First positive root

3 Answers3

Linked

Related