Problem using ArcTan inside NDSolve

Question

I'm messing around a bit with using "thrust segments" on a point-mass in NDSolve and have run into a strange problem to do with using ArcTan inside NDSolve. The code below applies thrust to a point-mass for 30 seconds, and then lets it move in free-fall from then onward.

Remove["Global`*"]
g = 9.81; (*Gravitational acceleration*)
m0 = 50000; (*Initial mass*)
T = 1200000;(*Thrust*)
Isp = 300; (*Specific impulse*)
tmax = 1000;(*Maximum value for t*)
theta = 177;(*Thrust angle*)

Solution = NDSolve[{
   x''[t] == If[t < 30, T/m[t] Cos[theta Degree], 0],
   y''[t] == If[t < 30, T/m[t] Sin[theta Degree], 0] - g, 
   m'[t] == If[t < 30, -(T/(g Isp)), 0],
   gamma[t] == ArcTan[x'[t], y'[t]],
   x[0] == 100000, y[0] == 100000, x'[0] == 1900 Cos[70 Degree], 
   y'[0] == 1900 Sin[70 Degree], m[0] == m0}, {x[t], y[t], x'[t], 
   y'[t], m[t], gamma[t]}, {t, 0, tmax}, MaxSteps -> 1000000]


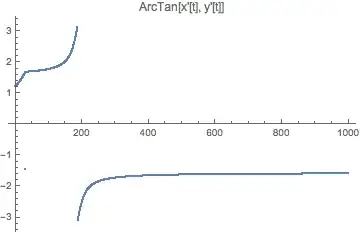
gammatable = Table[ArcTan[x'[t], y'[t]]*180/\[Pi] /. Solution, {t, 0, tmax}]

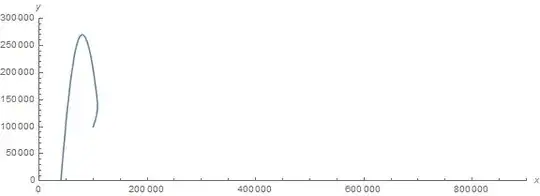
ParametricPlot[Evaluate[{x[t], y[t]} /. Solution], {t, 0, tmax}, 
 AxesLabel -> {x, y}, PlotRange -> {{0, 900000}, {0, 300000}}, 
 PlotStyle -> Automatic, ImageSize -> Large]
Animate[ParametricPlot[Evaluate[{x[t], y[t]} /. Solution], {t, 0, a}, 
  AxesLabel -> {x, y}, PlotRange -> {{0, 900000}, {0, 300000}}, 
  PlotStyle -> Automatic, ImageSize -> Large], {a, 0, tmax}, 
 AnimationRate -> 5, AnimationRepetitions -> 1]

As can be seen, a term called gamma is calculated inside NDSolve, which is just the flight-path angle of the point mass, gamma[t] == ArcTan[x'[t], y'[t]]. It seems that when the y-velocity of the particle becomes zero (at the top of the free-fall arc), the calculation of gamma goes haywire and the subsequent plot and animation "break". Looking at the values that gamma attains at the point where the y-velocity is zero (produced using gammatable), we see that the value of ArcTan is very close to zero. However, from then onward the value stays close to zero, even though the particle gains negative y-velocity. As such, I'm wondering if there's a way to prevent this from happening so that an accurate value for gamma is given at each point in time from t = 0 to t = tmax. I tried using the following gamma[t] == If[y'[t] < Abs[0.01], \[Pi], ArcTan[x'[t], y'[t]]], which seemed to fix the problem. However this quick-fix is less than ideal and I was hoping there there is a cleaner way using no tricks to fix the problem. Any help would be great, thanks!

Are you sure you want to be using "remove"? The basic methods for stiffness switching unfortunately don't work here. — Feyre, Jul 24 '16 at 20:18

Young · Answer 1 · 2016-07-24T23:08:59.433

One of the methods I've used with stiff systems is to reduce the PrecisionGoal (and sometimes AccuracyGoal). Check the result for reasonableness.

Solution = NDSolve[{
    x''[t] == If[t < 30, T/m[t] Cos[theta Degree], 0],
    y''[t] == If[t < 30, T/m[t] Sin[theta Degree], 0] - g,
    m'[t] == If[t < 30, -(T/(g Isp)), 0],
    gamma[t] == ArcTan[x'[t], y'[t]],
    x[0] == 100000, y[0] == 100000, x'[0] == 1900 Cos[70 Degree], 
    y'[0] == 1900 Sin[70 Degree], m[0] == m0},
   {x[t], y[t], x'[t], y'[t], m[t], gamma[t]}, {t, 0, tmax}, 
   MaxSteps -> Infinity, PrecisionGoal -> 1, AccuracyGoal -> 10];

arc = Table[
   ParametricPlot[Evaluate[{x[t], y[t]} /. Solution], {t, 0, a}, 
    AxesLabel -> {x, y}, PlotRange -> {{0, 300000}, {0, 300000}}, 
    PlotLabel -> a, PlotStyle -> Automatic, ImageSize -> Large], 
   {a, 1, 400}];
Export["arc.gif", arc]

Note:
The above result agrees with gamma[t] == If[y'[t] < Abs[0.01], \[Pi], ArcTan[x'[t], y'[t]]]

Michael E2 · Accepted Answer · 2016-07-25T05:20:59.230

3

One way to avoid the discontinuity of the branch cut in ArcTan is to integrate its derivative. This also converts the DAE, which is restricted to use the IDA method, to an ODE. This allows greater flexibility in integrating the system. In this case, the default settings seem to work well as is.

g = 9.81;      (*Gravitational acceleration*)
m0 = 50000;    (*Initial mass*)
T = 1200000;   (*Thrust*)
Isp = 300;     (*Specific impulse*)
tmax = 1000;   (*Maximum value for t*)
theta = 177;   (*Thrust angle*)
{Solution} = 
 NDSolve[{     (* Piecewise[] is a better choice than If[] for functions/equations *)
   x''[t] == Piecewise[{{T/m[t] Cos[theta Degree], t < 30}}], 
   y''[t] == Piecewise[{{T/m[t] Sin[theta Degree], t < 30}}] - g, 
   m'[t] == Piecewise[{{-(T/(g Isp)), t < 30}}],
   gamma'[t] == D[ArcTan[x'[t], y'[t]], t],        (* <-- N.B. *)
   x[0] == 100000, y[0] == 100000,
   x'[0] == 1900 Cos[70 Degree], y'[0] == 1900 Sin[70 Degree],
   m[0] == m0,
   gamma[0] == 70 Degree},                         (* <-- N.B. *)
  {x, y, m, gamma}, {t, 0, tmax}]

gammatable = Table[ArcTan[x'[t], y'[t]] /. Solution, {t, 0, tmax}];

Plot of gamma[t]:

Plot[Evaluate[gamma[t] /. Solution], {t, 0, tmax}]

Mathematica graphics

Compare with the original idea for gamma[t] as ArcTan[x'[t], y'[t]]:

ListPlot@gammatable

Mathematica graphics

Aside from a glitch at the discontinuity in the ODE at t == 30, there is a discontinuity in ArcTan[x'[t], y'[t]] around t == 186, which is where the OP's original NDSolve[] ran into a stiffness/singularity problem (NDSolve::ndsz).

ParametricPlot[Evaluate[{x[t], y[t]} /. Solution], {t, 0, tmax}, 
 AxesLabel -> {x, y}, PlotRange -> {{0, 300000}, {0, 300000}}]

Mathematica graphics

edited Jul 25 '16 at 05:20

answered Jul 25 '16 at 04:50

Michael E2

235,386
17
334
747

Nice ... Ultimately it looks like the same answer. – Young Jul 25 '16 at 05:08
@Young They shouldn't be too far apart. It's hard to say what is the net effect of reducing PrecisionGoal and raising AccuracyGoal (in your method). Theoretically, PrecisionGoal -> 1 would allow as much as a ~10% error in a local step, but the two solutions do not appear that far off from each other. – Michael E2 Jul 25 '16 at 05:19
Very nice little "trick", works like a charm. – InquisitiveInquirer Jul 25 '16 at 10:12
As an aside, do you know why Piecewise is better than using If in this situation? – InquisitiveInquirer Jul 25 '16 at 11:53
@user7388 Piecewise is intended for constructing functions and If is for programming (control flow). In particular, solvers treat the boundaries of cases in Piecewise as potential discontinuities and adapt the solving method to the discontinuities. This is important because error estimators generally assume the function has continuous derivatives up to some order (depending on the order of the method). In recent versions, some/all solvers seem to handle some If statements, so my advice is perhaps less important now. It's more of a precaution. – Michael E2 Jul 25 '16 at 14:40
@user7388 BTW, NDSolve seems to handle the If[] in this particular case. Simple, non-DE example: Compare Plot[(*PiecewiseExpand@*)If[x < 2, 1, 2], {x, 0, 4}] with the uncommented PiecewiseExpand@. – Michael E2 Jul 25 '16 at 14:43
Instead of asking a new question I thought maybe I should try and ask it here. Would you possibly know how to add a red dot to the animation that follows the animation's "tip" when thrust is being applied? – InquisitiveInquirer Jul 26 '16 at 15:30

Problem using ArcTan inside NDSolve

2 Answers2

Linked