Strange results from NDSolve after using a smooth (Tanh) function to approximate a discontinuous (jump) event

Question

I am solving a system of ODE which contains a discontinuous ode (the equation v[t]== ...in the following code and it means that my v[t] jumps between vmax (i.e.,2.25) and 0).

After a long time of trial and error (try to solve the odes system by using If, PieceWise, UnitStep, etc), I found that WhenEvent successfully gives me a reasonable result (sol1 in my code).

Then I tried to solve my system of ode by using smooth function of (Tanh) to approximate the discontinuous ode, and then I manually converted the algebraic equation to an ode by taking derivative with respect to time as in this post. This time I solved the odes much faster, but I got a very different and unreasonable result (sol2 in my code).

My code is shown below.

Why are these results (i.e., sol1 by using event and sol2 by converting to odes ) so different? What's wrong with my sol2? Is it beacuse of my converting the algebraic equation of v[t] to a ode? Or Tanh function not approroate here?

Thanks.

My code:

Remove["Global`*"] // Quiet;

tend = 2;
tdat = Range[0, tend, 0.01];
gdat =(*RandomVariate[NormalDistribution[0,0.5],Length[tdat]]*)
  2 Exp[-0.5 tdat] Sin[100 tdat]^2 Cos[50 tdat]^3;
tgdat = {tdat, gdat}\[Transpose];
xg = Interpolation[tgdat, InterpolationOrder -> 1];
(*Plot[xg[t],{t,0,tend},PlotRange\[Rule]All];*)

m = {{98.3, 0, 0}, {0, 98.3, 0}, {0, 0, 98.3}};
c = {{175, -50, 0}, {-50, 100, -50}, {0, -50, 50}};
k = {{12, -6.84, 0}, {-6.84, 13.7, -6.84}, {0, -6.84, 6.84}} 10^5;
x = {x1[t], x2[t], x3[t]};
dx = {x1'[t], x2'[t], x3'[t]};
ddx = {x1''[t], x2''[t], x3''[t]};

Α = 301;
n = 2;
η = 190;

vmax = 2.25;
αs[u_] := 140 10^2 + 695 10^2 u;
c1[u_] := 283 10^2 + 2.95 10^2 u;
c0[u_] := 21 10^2 + 3.5 10^2 u;
f[u_, dy_, x1_] := c1[u] dy + 500 (x1 - 0);
fc[x1_, x2_, x3_, v1_, v2_, v3_] := 
  4 10^6 x1 - 3.4 10^6 x2 + 752341 x3 + 37284 v1 + 26262 v2 + 7604 v3;

sol1 = NDSolve[{
      Flatten[m.ddx + c.dx + k.x] == 
       Flatten[-m.{1, 1, 1} xg[t] + {-1, 0, 0} f[u[t], y'[t], 
           x1[t]]],
      z'[t] == -50 10^4 Sqrt[(x1'[t] - y'[t])^2] z[t] Sqrt[z[t]^2] - 
        363 10^4 (x1'[t] - y'[t]) z[
          t]^2 + Α (x1'[t] - y'[t]),
      y'[t] == 
       1/(c0[u[t]] + 
         c1[u[t]]) (αs[u[t]] z[t] + c0[u[t]] D[x1[t], t] + 
          4690 (x1[t] - y[t])),
      WhenEvent[(fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - 
           f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] < 0, 
       v[t] -> 0],
      WhenEvent[(fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - 
           f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] > 0, 
       v[t] -> 2.25],
      u'[t] == -η (u[t] - v[t]),
      v[0] == 0, u[0] == 0, z[0] == 0, y[0] == 0, 
      x1[0] == x1'[0] == 0, x2[0] == x2'[0] == 0, 
      x3[0] == x3'[0] == 0} // Flatten,
    {y, z, v, u, x1, x2, x3}, {t, 0, tend}
    , Method -> {"EquationSimplification" -> "Residual"}
    , MaxSteps -> Infinity
    , DiscreteVariables -> v[t]] // Flatten;
sol2 = NDSolve[{
      Flatten[m.ddx + c.dx + k.x] == 
       Flatten[-m.{1, 1, 1} xg[t] + {-1, 0, 0} f[u[t], y'[t], 
           x1[t]]],
      z'[t] == -50 10^4 Sqrt[(x1'[t] - y'[t])^2] z[t] Sqrt[z[t]^2] - 
        363 10^4 (x1'[t] - y'[t]) z[
          t]^2 + Α (x1'[t] - y'[t]),
      y'[t] == 
       1/(c0[u[t]] + 
         c1[u[t]]) (αs[u[t]] z[t] + c0[u[t]] D[x1[t], t] + 
          4690 (x1[t] - y[t])),
      v'[t] == 
       D[vmax (1 + 
          Tanh[2000 (fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] -
               f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]]])/2, t],
      (*v[t]=vmax Simplify`PWToUnitStep@Piecewise[{{0,(fc[x1[t],x2[t],
      x3[t],x1'[t],x2'[t],x3'[t]]-f[u[t],y'[t],x1[t]])f[u[t],y'[t],x1[
      t]]≤ 0}},vmax],*)

      u'[t] == -η (u[t] - v[t]),
      v[0] == 0, u[0] == 0, z[0] == 0, y[0] == 0, 
      x1[0] == x1'[0] == 0, x2[0] == x2'[0] == 0, 
      x3[0] == x3'[0] == 0} // Flatten,
    {y, z, v, u, x1, x2, x3}, {t, 0, tend}
    , MaxSteps -> Infinity] // Flatten;
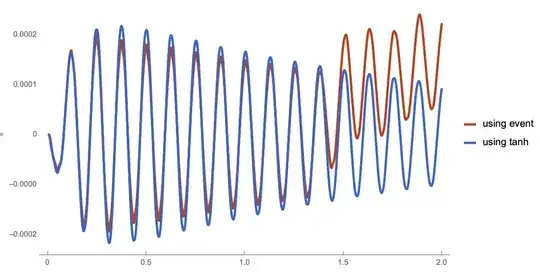
Plot[u[t] /. {sol1, sol2} // Evaluate, {t, 0, tend}, PlotRange -> All,
  PlotTheme -> "Web", PlotLegends -> {"using event", "using tanh"}]
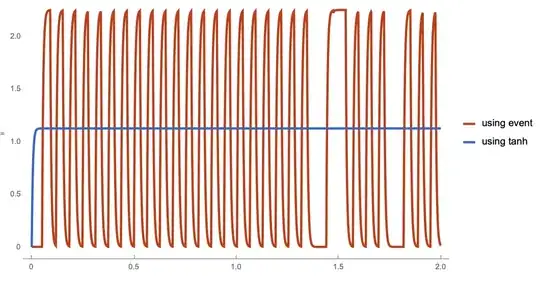
Plot[v[t] /. {sol1, sol2} // Evaluate, {t, 0, tend}, PlotRange -> All,
  PlotTheme -> "Web", PlotLegends -> {"using event", "using tanh"}]
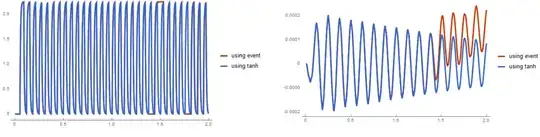
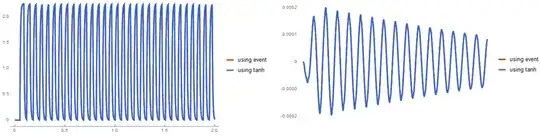
Plot[y[t] /. {sol1, sol2} // Evaluate, {t, 0, tend}, PlotRange -> All,
  PlotTheme -> "Web", PlotLegends -> {"using event", "using tanh"}]

Change your second WhenEvent v[t]->2.25 to v[t]->1 ! Now the solutions sol1 an sol2 are the same! — Ulrich Neumann, Nov 09 '19 at 14:05
Thanks. I tried your suggestion, but sol1 is still apparently different from sol1 (for example u[t] of sol1 and sol2). BTW, why did you suggest that changing v[t]->2.25 to v[t]->1 ? my vmax is 2.25, not 1, and it jumps between 0 and vmax(2.25). — xinxin guo, Nov 09 '19 at 14:12
Sorry I didn't recognize vmax in sol2. Setting v[t]->1gives a good match of sol1 and sol2 in your second last plot (don't know why) — Ulrich Neumann, Nov 09 '19 at 14:17
Thanks. Acctually the most important result to me is u[t]. — xinxin guo, Nov 09 '19 at 14:22
You might want to plot fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] versus v[t] to see if every event was captured by NDSolve. — Michael E2, Nov 09 '19 at 17:33
I don't see why NDSolve should fail to detect the events. I think it's a bug. Please report it to WRI support. — Michael E2, Nov 09 '19 at 21:12
@Michael E2 Thanks for attentions. I don't think it is a bug and adding "LocationMethod" -> "LinearInterpolation" is helpful, as documented in the builtin reference of NDSolve. — xinxin guo, Nov 10 '19 at 11:35

Alex Trounev · Accepted Answer · 2019-11-09T19:25:21.203

These are different systems of equations. You can coordinate them by removing equation v'[t]== in the second system and replacing v[t] to If[t < 0.05050561921089747, 0, vmax (1 + Tanh[.01 (fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]]])/2]. Then the solutions coincide up to t = 1.37, but then diverge.

tend = 2;
tdat = Range[0, tend, 0.01];
gdat =(*RandomVariate[NormalDistribution[0,0.5],Length[tdat]]*)
  2 Exp[-0.5 tdat] Sin[100 tdat]^2 Cos[50 tdat]^3;
tgdat = {tdat, gdat}\[Transpose];
xg = Interpolation[tgdat, InterpolationOrder -> 1];
(*Plot[xg[t],{t,0,tend},PlotRange\[Rule]All];*)

m = {{98.3, 0, 0}, {0, 98.3, 0}, {0, 0, 98.3}};
c = {{175, -50, 0}, {-50, 100, -50}, {0, -50, 50}};
k = {{12, -6.84, 0}, {-6.84, 13.7, -6.84}, {0, -6.84, 6.84}} 10^5;
x = {x1[t], x2[t], x3[t]};
dx = {x1'[t], x2'[t], x3'[t]};
ddx = {x1''[t], x2''[t], x3''[t]};

\[CapitalAlpha] = 301;
n = 2;
\[Eta] = 190;

vmax = 2.25;
\[Alpha]s[u_] := 140 10^2 + 695 10^2 u;
c1[u_] := 283 10^2 + 2.95 10^2 u;
c0[u_] := 21 10^2 + 3.5 10^2 u;
f[u_, dy_, x1_] := c1[u] dy + 500 (x1 - 0);
fc[x1_, x2_, x3_, v1_, v2_, v3_] := 
  4 10^6 x1 - 3.4 10^6 x2 + 752341 x3 + 37284 v1 + 26262 v2 + 7604 v3;

sol1 = NDSolve[{Flatten[m.ddx + c.dx + k.x] == 
       Flatten[-m.{1, 1, 1} xg[t] + {-1, 0, 0} f[u[t], y'[t], x1[t]]],
       z'[t] == -50 10^4 Sqrt[(x1'[t] - y'[t])^2] z[t] Sqrt[z[t]^2] - 
        363 10^4 (x1'[t] - y'[t]) z[t]^2 + \[CapitalAlpha] (x1'[t] - 
           y'[t]), 
      y'[t] == 
       1/(c0[u[t]] + c1[u[t]]) (\[Alpha]s[u[t]] z[t] + 
          c0[u[t]] D[x1[t], t] + 4690 (x1[t] - y[t])), 
      WhenEvent[(fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - 
           f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] < 0, 
       v[t] -> 0], 
      WhenEvent[(fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - 
           f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] > 
        0, v[t] -> vmax], u'[t] == -\[Eta] (u[t] - v[t]), 
      v[0] == 0, u[0] == 0, z[0] == 0, y[0] == 0, 
      x1[0] == x1'[0] == 0, x2[0] == x2'[0] == 0, 
      x3[0] == x3'[0] == 0} // Flatten, {y, z, v, u, x1, x2, x3}, {t, 
     0, tend}, Method -> {"EquationSimplification" -> "Residual"}, 
    MaxSteps -> Infinity, DiscreteVariables -> v[t]] // Flatten;
sol2 = NDSolve[{Flatten[m.ddx + c.dx + k.x] == 
       Flatten[-m.{1, 1, 1} xg[t] + {-1, 0, 0} f[u[t], y'[t], x1[t]]],
       z'[t] == -50 10^4 Sqrt[(x1'[t] - y'[t])^2] z[t] Sqrt[z[t]^2] - 
        363 10^4 (x1'[t] - y'[t]) z[t]^2 + \[CapitalAlpha] (x1'[t] - 
           y'[t]), 
      y'[t] == 
       1/(c0[u[t]] + c1[u[t]]) (\[Alpha]s[u[t]] z[t] + 
          c0[u[t]] D[x1[t], t] + 4690 (x1[t] - y[t])), u'[t] == -\[Eta] (u[t] - 
          If[t < 0.05050561921089747, 0, 
           vmax (1 + 
               Tanh[.01 (fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], 
                    x3'[t]] - f[u[t], y'[t], x1[t]]) f[u[t], y'[t], 
                  x1[t]]])/2]), u[0] == 0, z[0] == 0, y[0] == 0, 
      x1[0] == x1'[0] == 0, x2[0] == x2'[0] == 0, 
      x3[0] == x3'[0] == 0} // Flatten, {y, z, u, x1, x2, x3}, {t, 0, 
     tend}, MaxSteps -> Infinity, 
    Method -> {"EquationSimplification" -> "Residual"}] // Flatten;
Plot[u[t] /. {sol1, sol2} // Evaluate, {t, 0, tend}, PlotRange -> All,
  PlotTheme -> "Web", PlotLegends -> {"using event", "using tanh"}]

Plot[y[t] /. {sol1, sol2} // Evaluate, {t, 0, tend}, PlotRange -> All,
  PlotTheme -> "Web", PlotLegends -> {"using event", "using tanh"}]

We can achieve a complete match if we put in the first system

WhenEvent[(fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], x3'[t]] - 
     f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] < 10^-3, 
 v[t] -> 0], WhenEvent[(fc[x1[t], x2[t], x3[t], x1'[t], x2'[t], 
      x3'[t]] - f[u[t], y'[t], x1[t]]) f[u[t], y'[t], x1[t]] > -1, v[t] -> vmax]

Did you mean "but then diverge"? It looks like an event was missed around t = 1.37 and a couple of times after that. Could be the reason for the divergence. — Michael E2, Nov 09 '19 at 17:30
Thanks. I found that If[t < 10^-5, .... also produced almost the same result as yours, so it seems that the two systems only different in the initial conditions. I think this more. — xinxin guo, Nov 09 '19 at 18:22
@MichaelE2 You're right, I corrected for diverge. Obviously the difference in the missed event. Found that this is due to an error in calculation fc. — Alex Trounev, Nov 09 '19 at 19:11
@ Alex Trounev, thanks, your answer is very helpful and makes me find many more interesting aspects of NDSolve. I really appreciate your time helping many Mathematica fans. Have a nice day :) — xinxin guo, Nov 10 '19 at 11:37

Strange results from NDSolve after using a smooth (Tanh) function to approximate a discontinuous (jump) event

1 Answers1

Linked