How to label ticks in ListLogLogPlot in scientific form in MMA 10.4?

Question

This is a question regarding ListLogLogPlot in MMA 10.4. I have tried the solutions suggested in 5369, and they do not appear to work in MMA 10.4, so I would be grateful if this could be considered a new question by the moderators.

Using LogPlot with no tick label formatting, one gets:

LogLogPlot[Log[x!+1], {x, 1, 10^5}, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}]

Custom labels for the ticks can be added with:

LogLogPlot[Log[x! + 1], {x, .1, 10^5}, PlotRange -> {{.1, 10^5}, 
  {10^-1, 10^6}}, Ticks -> {Table[{10^i, 10^Defer[Evaluate[i]]}, 
  {i, -1, 5}], Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 6}]}]

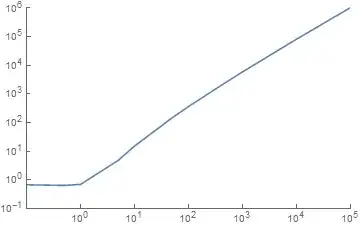
So far so good. Now with ListLogLogPlot, and no custom tick label formating, we get:

plist = {#, 1. Log[#! + 1]} & /@ {.1, .5, 1, 5, 10, 50, 100, 500, 
     1000, 5000, 10000, 50000, 100000};

ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
  Joined -> True]

Now try the custom tick labels, identical to those used above with LogLogPlot:

ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
  Ticks -> {Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 5}], 
  Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 6}]}, Joined -> True]

I have tried text labels in the {value,label} form without any luck. Post 5369 suggests a hack to modify the plot after generation, also no joy.

Thanks!

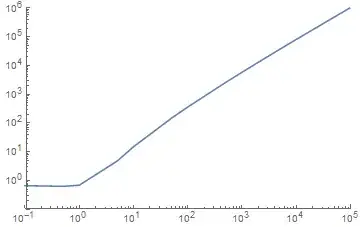
UPDATE - Looks like this has been fixed in Mathematica 11.0.

ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
   Ticks -> {Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 5}], 
   Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 6}]}, Joined -> True]

I see now that this is a bug in 10.4 regarding ListLogLogPlot rather than an intentional change. Would you instead give me the output of Options[ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, Joined -> True], {Ticks, FrameTicks}] on your system? — Mr.Wizard, Jul 24 '16 at 22:18
@Mr.Wizard I can confirm the last plot on 10.4. Requested output is Ticks -> {{{-2.30259, 0.1, {0.01, 0.}, {AbsoluteThickness[0.1]}}... and FrameTicks -> {{{{-2.30259, 0.1, {0.01, 0.}, {AbsoluteThickness[0.1]}} ... — Johu, Jul 24 '16 at 22:30
@Johu Thank you. Do you mind answering a few more questions for me? If so what is the output from Options[ LogLogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, 1, 10000}, Frame -> True], {Ticks, FrameTicks} ] — Mr.Wizard, Jul 24 '16 at 22:33
@Mr.Wizard {Ticks -> {Charting`ScaledTicks[{Log, Exp}], Charting`ScaledTicks[{Log, Exp}]}, FrameTicks -> {{Charting`ScaledTicks[{Log, Exp}], Charting`ScaledFrameTicks[{Log, Exp}]}, {Charting`ScaledTicks[{Log, Exp}], Charting`ScaledFrameTicks[{Log, Exp}]}}} — Johu, Jul 24 '16 at 23:03
@Johu Thanks, again. FYI you need to use two backticks to open and close a code-block that itself contains backtick. I edited your comment above (scary moderator power, I know) to correct this. Odd that ListLogLogPlot does not follow the convention of all the other plots to use Charting`ScaledTicks and Charting`ScaledFrameTicks as it did in version 10.1.0, and as LogLogPlot still does in 10.4 from your assistance. — Mr.Wizard, Jul 24 '16 at 23:06

Johu · Answer 1 · 2016-07-24T22:02:17.563

6

I tested on 10.2 and 10.4. I recommend just using the tick labels from some other plot and overlaying the data using Show. With minimal changes to your example I got following proof of principle.

plist = {#, 1. Log[#! + 1]} & /@ {.1, .5, 1, 5, 10, 50, 100, 500, 
    1000, 5000, 10000, 50000, 100000};

Show[{LogLogPlot[0, {x, .1, 10^5}, 
   PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
   Ticks -> {Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 5}], 
     Table[{10^i, 10^Defer[Evaluate[i]]}, {i, -1, 6}]}], 
  ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
   Joined -> True]}]

edited Jul 24 '16 at 22:02

answered Jul 24 '16 at 21:54

Johu

4,918
16
43

Very nice!! Thank you!! This is much simpler and more elegant than some of the previous answers to other similar questions. Still, it would be good if this bug was fixed so one did not have to resort to such hacks.... – GraphMan Jul 24 '16 at 22:00
1

If you want to contribute to getting a fix turn your post into a bug report and report to WR. – Johu Jul 24 '16 at 22:01
Done! Thanks again. – GraphMan Jul 24 '16 at 22:06

Karsten7 · Accepted Answer · 2016-07-25T13:19:39.857

4

Here is one way to convert the ticks into the desired format:

ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, Joined -> True] /. 
 {v_, t_?NumberQ, l1_, {AbsoluteThickness[0.1]}} :> 
 {v, NumberForm[N@t, NumberFormat -> (Superscript[#2, #3] &), 
  ExponentFunction -> (# &)], l1, {AbsoluteThickness[0.1]}}

With ticks outside and explicitly setting the AxesOrigin to get axes that are more aligned:

f[s_Spacer | s_Superscript] := s

f[n_Real | n_Integer] := Superscript[10, Rationalize@Log10[n]]

ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
  Joined -> True, AxesOrigin -> {0.1, 0.1}] /. {v_, t_, l1_, l2_} :> {v, f[t], -l1, l2}

edited Jul 25 '16 at 13:19

answered Jul 25 '16 at 01:11

Karsten7

27,448
5
73
134

Nice solution. I like that the sub-ticks still appear. Is it possible to reverse the tick orientation (towards the outside of the plot) for major and minor ticks with a modification of the script? – GraphMan Jul 25 '16 at 11:28
@GraphMan Orientation reversion by additional replacement: ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, Joined -> True] /. {v_, t_?NumberQ, l1_, {AbsoluteThickness[0.1]}} :> {v, NumberForm[N@t, NumberFormat -> (Superscript[#2, #3] &), ExponentFunction -> (# &)], l1, {AbsoluteThickness[0.1]}} /. {v_, t_, l1_, l2_} :> {v, t, -l1, l2} – Karsten7 Jul 25 '16 at 11:52
This solution does works only on 10.4 due to replacement rule of the form {v_, t_?NumberQ, l1_, {AbsoluteThickness[0.1]}}. Is there a similar soltuion for 10.3? For information Options[ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, Joined -> True], {Ticks, FrameTicks}] gives {Ticks -> {Charting`ScaledTicks[{Log, Exp}], Charting`ScaledTicks[{Log, Exp}]}, FrameTicks -> {{Charting`ScaledTicks[{Log, Exp}], Charting`ScaledFrameTicks[{Log, Exp}]}, {Charting`ScaledTicks[{Log, Exp}], Charting`ScaledFrameTicks[{Log, Exp}]}}} – Johu Aug 03 '16 at 13:38
@Johu Did you see the Update 2015 section in this answer? – Karsten7 Aug 03 '16 at 13:50
ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, Joined -> True] /. {v_, t_?NumberQ, l1_, l2_} :> {v, NumberForm[N@t, NumberFormat -> (Superscript[#2, #3] &), ExponentFunction -> (# &)], l1, l2} works in version 9. – Karsten7 Aug 03 '16 at 13:50

score 2 · Answer 3 · answered Jul 25 '16 at 10:48

Using custom tick labels still works, but one has to use the logarithmic label position, as this conversion is no longer done automatically for custom tick labels.

ListLogLogPlot[plist, PlotRange -> {{.1, 10^5}, {10^-1, 10^6}}, 
 Ticks -> {Table[{N@Log[10^i], Superscript[10, i]}, {i, -1, 5}], 
           Table[{N@Log[10^i], Superscript[10, i]}, {i, -1, 6}]}, 
 Joined -> True]

How to label ticks in ListLogLogPlot in scientific form in MMA 10.4?

3 Answers3

Linked