About the number format in ticks

Question

I want to LogPlot a function, but I have the trouble in the number format in the ticks.

For example,

LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10},
   Frame -> True, FrameTicks -> {{Automatic, None}, {None, None}}]

The output is

If I use the command

LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True,  
  FrameTicks -> {
    {{#, HoldForm[#]} & /@ {10^0, 10^-1, 10^-2, 10^-3, 10^-4, 10^-5}, None},
    {None, None}
   }
]

I can get

Actually, I prefer the all the ticks in the form of 10^n, and none of the commands shown above works.

Is there any simple and clever way to cope with it? I'll be grateful for your reply.

Answer 1

Perhaps this?

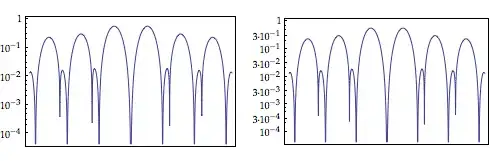
LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True, 
 FrameTicks -> {{{#, Superscript[10, Log10@#]} & /@ ({10^0, 10^-1, 
       10^-2, 10^-3, 10^-4, 10^-5}), None}, {None, None}}]

---

Here's a completely different approach, manipulating the existing tick labels in the generated graph, and preserving the unlabeled ticks. This seems much cleaner to me than Peter's approach, assuming that it works on version 8 as it does on version 7.

format =
  Replace[#, {p_, n_?NumericQ} :> {p, Superscript[10, Round@Log10@n]}, {#2}] &;

ticks = MapThread[format, {Options[#, {Ticks, FrameTicks}], {3, 4}}] &;

Use:

p = LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True];

Show[p, ticks[p]]

---

Update 2015

The new Ticks subsystem

Recent versions of Mathematica use a different ticks rendering system wherein functions specified for Ticks or FrameTicks are passed to the Front End (which calls the Kernel) rather than being evaluated beforehand. If we look at the options of p above we now see:

Options[p, {Ticks, FrameTicks}]

{
 Ticks -> {Automatic, Charting`ScaledTicks[{Log, Exp}]}, 
 FrameTicks -> {{Charting`ScaledTicks[{Log, Exp}], 
    Charting`ScaledFrameTicks[{Log, Exp}]}, {Automatic, Automatic}}
}

We could use these functions to compute tick specifications external to plotting, but to follow the spirit of the new paradigm we can modify the output of these functions instead.

ScaledTicks returns (at least?) three different label formats which we must handle:

Charting`ScaledTicks[{Log, Exp}][-11.7, 1.618][[2 ;; 4, 2]] // InputForm

{Superscript[10, -4], 0.001, NumberForm[0.01, {Infinity, 3}]}

The Superscript is already our desired format. The other two may be handled with replacement:

format2 =
  Replace[#, n_?NumericQ | NumberForm[n_, _] :> Superscript[10, Round@Log10@n]] &;

We can then use this to apply the formatting:

relabel = # /. CST_Charting`ScaledTicks :> (MapAt[format2, CST[##], {All, 2}] &) &;

LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}] // relabel

relabel also works with framed plots.

Spelunking internal functions

One may be interested is the source of the original label formatting. Charting`ScaledTicks calls:

Charting`SimplePadding

which takes the option "CutoffExponent" which we would like to use, but unfortunately ScaledTicks overrides it. If we use:

ClearAttributes[Charting`ScaledTicks, {Protected, ReadProtected}]

And then modify the definition to replace:

"CutoffExponent" -> 
 If[{Visualization`Utilities`ScalingDump`f, 
    Visualization`Utilities`ScalingDump`if} === {Identity, Identity}, 6, 4]

With:

"CutoffExponent" -> 1

We will find that the desired formatting has been effected:

LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True]

This modification is inadvisable however, and sadly Charting`ScaledTicks does not itself take "CutoffExponent" as an option that would be passed on. One could modify its definition to add this option, but it is safer to use relabel defined above.

Answer 2

If you want the minor ticks too, you can use the following function:

SetAttributes[dtZahl, Listable]
dtZahl[x_] := Block[{n}, If[IntegerQ[n = Rationalize[x]], n, x]]

exponentForm[x_?NumberQ] := 
  Module[{me = MantissaExponent[x], num, exp}, 
   If[MemberQ[{0, 0., 1, 1., -1, -1.}, x], Return[IntegerPart[x]]];
   exp = Superscript["\[CenterDot]10", me[[2]] - 1];
   num = NumberForm[N[me[[1]]]*10 // dtZahl, 3];
   If[me[[1]] == 0.1,(*no mantissa*)num = "";
    exp = Superscript[10, me[[2]] - 1], 
    If[me[[2]] == 1,(*range 0..10*)exp = ""]];
   Row[{num, exp}]];
exponentForm[x_] := x

Options[logTicks] = {TicksFaktor -> 1};
logTicks[von_Integer, bis_Integer, werte_List, subwerte_List, 
  OptionsPattern[]] :=
 Module[{mt, st, ticks, res, tf},
  tf = OptionValue[TicksFaktor];
  mt = {#, exponentForm[N[#]], {0.01, 0}*tf} & /@ 
    Flatten@Table[10^i*werte, {i, von, bis}];
  st = {#, Null, {0.005, 0}*tf} & /@ 
    Flatten@Table[10^i*subwerte, {i, von, bis}];
  Join[mt, st]]

logTicks takes the following Parameters:
von and bis are the lowest and highest exponent. The list werte is the list of labeled ticks in one decade and subwerte the list of unlabeled ticks in one decade.

Example:

GraphicsRow[{
  ticks = logTicks[-4, 1, {1}, {2, 3, 5, 7}];
  LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True, 
   FrameTicks -> {{ticks, None}, {None, None}}],
  ticks = logTicks[-4, 1, {1, 3}, {2, 5, 7}];
  LogPlot[Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True, 
   FrameTicks -> {{ticks, None}, {None, None}}]
  }]

Output:

Answer 3

Is there any simple and clever way to cope with it?

Why yes there is, just use the CustomTicks package,

Needs@"CustomTicks`";
Plot[Log10@Abs[BesselJ[1, x] Sin[x]^2], {x, -10, 10}, Frame -> True, 
 FrameTicks -> {{LogTicks, None}, {None, None}}, Axes -> None]