Changing coordinates or rotating finished 3d Graphics

Question

I have created a 3d graphics consisting of three parts and I would now like to take the entire result and rotate it. Here is the code so far:

thick = 0.02;
surf = ParametricPlot3D[{a^2 + 2*a*(1 - a - b) + (1 - a - b)^2, b^2 + 2*b*(1 - a - b) + (1 - a - b)^2, 2*a*b + (1 - a - b)^2}, {a, b} \[Element] ImplicitRegion[{a >= 0, b >= 0, 1 - a - b >= 0}, {a, b}], Mesh -> None, PlotStyle -> Thickness[thick]]
curve2 = ParametricPlot3D[{a^2 + 2*a*(1 - a - (1 - a)) + (1 - a - (1 - a))^2, (1 - a)^2 + 2*(1 - a)*(1 - a - (1 - a)) + (1 - a - (1 - a))^2, 2*a*(1 - a) + (1 - a - (1 - a))^2}, {a, 0, 1}, PlotStyle -> Thickness[thick]]
simp = Graphics3D[{Cylinder[{{0, 0, 1}, {1, 0, 0}}, thick],    Cylinder[{{0, 0, 1}, {0, 1, 0}}, thick],    Cylinder[{{0, 0, 1}, {1, 1, 1}}, thick],    Cylinder[{{0, 1, 0}, {1, 0, 0}}, thick],   Cylinder[{{0, 1, 0}, {1, 1, 1}}, thick],    Cylinder[{{1, 0, 0}, {1, 1, 1}}, thick],   Sphere[{1, 1, 1}, thick],   Sphere[{0, 0, 1}, thick],   Sphere[{0, 1, 0}, thick],   Sphere[{1, 0, 0}, thick]}]

Then

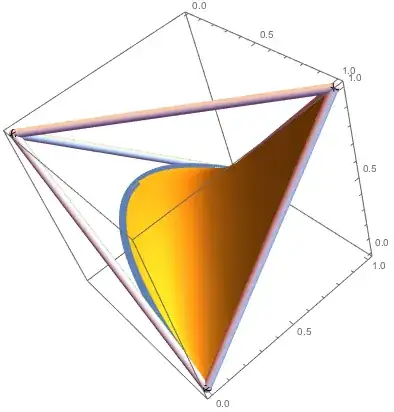
Show[surf, simp, curve2]

gives

Now my goal is to lie the simplex flat on the ground, which is a certain rotation around the vector {1,-1,0} if I'm not mistaken. I've tried various things with GeometricTransformation but it seems all those work only on primitives?