9

I'd like to find the volume of the region of intersection of the spheres defined by $$x^2+y^2+z^2=4$$ and: $$x^2+y^2+z^2+4x-2y+4z+5=0$$

I tried:

a = ImplicitRegion[
  x^2 + y^2 + z^2 + 4 x - 2 y + 4 z + 5 <= 0 && 
   x^2 + y^2 + z^2 <= 4, {x, y, z}]

Then I tried:

Volume[a]

But I had to abort.

Any suggestions?

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136
David
  • 14,883
  • 4
  • 44
  • 117
  • Ouch! I entered the wrong equation. In my code above I have $x^2+y^2+z^2+4x-2y+4x+5\le 0$. I entered $4x$ instead of $4z$. I should have entered $x^2+y^2+z^2+4x-2y+4z+5\le 0$ – David Sep 09 '16 at 05:39
  • @Xavier How about an exact answer, which should be $11\pi/12$ if I enter the correct inequality $x^2+y^2+z^2+4x-2y+4z+5\le0$. Any way to get this exact answer? – David Sep 09 '16 at 05:43
  • 1
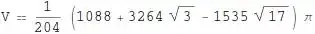
    I waited for Volume to finish. It doesn't give an answer. It is very strange that Boole and Integrate work but Volume doesn't. – Szabolcs Sep 09 '16 at 09:13

4 Answers4

10

Boole is a way:

V = Integrate[
 Boole[x^2 + y^2 + z^2 + 4 x - 2 y + 4 x + 5 <= 0 && 
   x^2 + y^2 + z^2 <= 4], {x, -∞, ∞}, {y, -∞, ∞}, {z, -∞, ∞}]

The result:

enter image description here

i.e., $V\approx 6.35166$.

EDIT: It seems I was lucky: after correcting the erroneous $x$ to $z$ the Integrate of Boole takes a ridiculously long time to return an enourmous integral over $x$. Nonetheless, the initial idea is still valid when one aims at obtaining an approximate result via NIntegrate:

v = NIntegrate[
 Boole[x^2 + y^2 + z^2 + 4 x - 2 y + 4 z + 5 <= 0 && 
   x^2 + y^2 + z^2 <= 4], {x, -∞, ∞}, {y, -∞, ∞}, {z, -∞, ∞}] // RepeatedTiming

{0.0581, 2.87979}

The above takes a comparable amount of time as Xavier's approach (i.e., 0.0414 on my computer).

EDIT2: I've tested every method from Can Mathematica propose an exact value based on an approximate one?, and only the Python script by Simon yielded as a result $\frac{11\pi}{12}$:

from mpmath import *
mp.dps = 15;
print identify(2.87979320312696707163, ['pi'])

pi*((264-sqrt(0))/288)

Community
  • 1
corey979
  • 23,947
  • 7
  • 58
  • 101
10

Update: Region equation changed after OP's edit.

In case you're only after a non-exact result, you can change the value of the option WorkingPrecision (by default Infinity for Volume) or change the method. These give a result pretty fast:

reg = ImplicitRegion[x^2 + y^2 + z^2 + 4 x - 2 y + 4 z + 5 <= 0 && 
                     x^2 + y^2 + z^2 <= 4, {x, y, z}]

RepeatedTiming[Volume[reg, WorkingPrecision -> MachinePrecision]]
(* {0.076, 2.87979} *)

RepeatedTiming[Volume[reg, Method -> "NIntegrate"]]
(* {0.078, 2.87979} *)
10

Correcting the $z-x $ issue and using 

Expand[(x + 2)^2 + (y - 1)^2 + (z + 2)^2] - 4 == 
 x^2 + y^2 + z^2 + 4 x - 2 y + 4 z + 5

yields true-> centres of spheres.

Therefore, using this to derive analytic solution: 

c = {-2, 1, -2};
Show[ContourPlot3D[{(x + 2)^2 + (y - 1)^2 + (z + 2)^2 == 4, 
   x^2 + y^2 + z^2 == 4}, {x, -4, 4}, {y, -4, 4}, {z, -4, 4}, 
  ContourStyle -> Opacity[0.5], Mesh -> None],
 Graphics3D[{Red, PointSize[0.04], Point[{{0, 0, 0}, c}], 
   Line[{{0, 0, 0}, c}]}
  ]]
r = 2;
R = 2;
vol[a_, b_] := Pi (4 a + b) (2 a - b)^2/12;
vol[R, Norm@c]

enter image description here

ubpdqn
  • 60,617
  • 3
  • 59
  • 148
6

Here's just one more way to get the answer,

NIntegrate[1, {x, y, z} ∈ RegionIntersection[
   Ball[{0, 0, 0}, 2],
   Ball[{-2, 1, -2}, 2]]]
(* 2.87979 *)

Sadly, 

Volume [RegionIntersection[
 Ball[{0, 0, 0}, 2],
 Ball[{-2, 1, -2}, 2]]

won't give an exact answer in any reasonable time in the same way that Area@RegionIntersection[Disk[{0, 0}, 2], Disk[{-2, 1}, 2]] does.

Jason B.
  • 68,381
  • 3
  • 139
  • 286