Region rotated about the line y=2

Question

Could a few people share the best way to display the image created by rotating the region bounded by $y=x^4$ and $y=1$ about the line $y=2$?

Thanks.

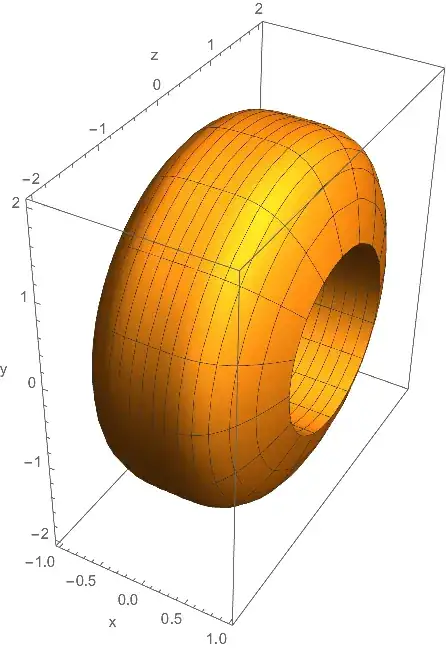
Update: I took JasonB's hint and tried this:

Show[
 RevolutionPlot3D[x^4 - 2, {x, -1, 1}, RevolutionAxis -> {1, 0, 0},
  AxesLabel -> {"x", "z", "y"}],
 RevolutionPlot3D[-1, {x, -1, 1}, RevolutionAxis -> {1, 0, 0}]
 ]

Which gave this image:

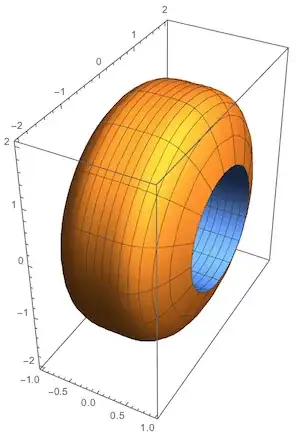
How can I change the ticks on the y-axis to run from 0, 1, 2, 3, and 4?

Thanks.

Second Update:

Looks like I found an answer to my tick question.

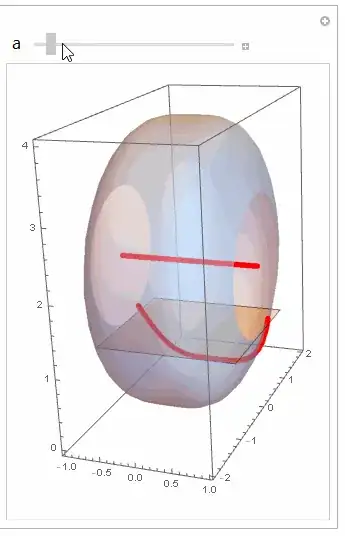
Manipulate[
 RevolutionPlot3D[{{x^4 - 2}, {1 - 2}}, {x, -1, 1}, {\[Theta], 0, 
   tau}, RevolutionAxis -> "X",
  PlotRange -> {{-1, 1}, {-2, 2}, {-2, 2}},
  AxesLabel -> {"x", "z", "y"},
  PerformanceGoal -> "Quality",
  Ticks -> {Automatic, 
    Automatic, {{-2, 0}, {-1, 1}, {0, 2}, {1, 3}, {2, 4}}}],
 {{tau, 0.1}, 0, 2 \[Pi]}]

@ChipHurst I would like to see an answer that uses RevolutionPlot3D. — David, Sep 23 '16 at 15:18

score 6 · Answer 1 · edited Apr 13 '17 at 12:55

One option is to define the 3D region you want to plot in terms of a set of boolean predicates and feed them to Simon Woods's contourRegionPlot3D (follow link for the code).

Here's the region you want to rotate

Plot[{x^4, 1}, {x, -1, 1}, PlotRangePadding -> 0.1, 
 Filling -> {1 -> {2}}]

Mathematica graphics

And here's the region plot

contourRegionPlot3D[
 1 <= z^2 + (y - 2)^2 <= (2 - x^4)^2 && -1 <= x <= 1,
 {x, -1.2, 1.2}, {y, -1, 5}, {z, -3, 3}]

Mathematica graphics

You can dress up the style as you see fit,

contourRegionPlot3D[
 1 <= z^2 + (y - 2)^2 <= (2 - x^4)^2 && -1 <= x <= 1,
 {x, -1.2, 1.2}, {y, -1, 5}, {z, -3, 3},
 Mesh -> None,
 Boxed -> False,
 Axes -> False,
 ContourStyle -> Directive[Blue, Opacity[0.6]],
 ImageSize -> 500]

score 4 · Answer 2 · edited Jun 16 '20 at 09:23

4

If you shift to rotate about $y = 0$, you can use RevolutionPlot3D.

RevolutionPlot3D[{{x^4 - 2}, {1 - 2}}, {x, -1, 1}, RevolutionAxis -> "X"]

Edit

The only I can think to correct the ticks (when using RevolutionPlot3D) is somewhat clunky...

a = 2;
plot = RevolutionPlot3D[{{x^4 - a}, {1 - a}}, {x, -1, 1}, RevolutionAxis -> "X"];
Show[
  plot /. g_GraphicsComplex :> Translate[g, {0, 0, a}],
  PlotRange -> All
]

edited Jun 16 '20 at 09:23

Community

1

answered Sep 23 '16 at 15:22

Greg Hurst

35,921
1
90
136

Thanks. This adds some more understanding for me. Can you check out the question in my update? How can I change the labels on the vertical axis to 0,1,2,3, and 4? – David Sep 23 '16 at 20:25
@David I updated my answer. I couldn't find a clean way to do it however. – Greg Hurst Sep 23 '16 at 21:51
Wow! Nice answer. – David Sep 24 '16 at 00:30
Looks like I've found an answer. See the second update to my original post. Thanks so much for the help. – David Sep 24 '16 at 00:36

score 2 · Answer 3 · answered Sep 22 '16 at 11:44

Just for fun:

pp = ParametricPlot3D[
   RotationMatrix[v, {1, 0, 0}].{u, 0, (u^4 - 2)} + {0, 0, 2}, {u, -1,
     1}, {v, 0, 2 Pi}, 
   PlotStyle -> {{LightBlue, Opacity[0.5]}, Directive[Red, Thick]}, 
   Mesh -> None];
plane = Plot3D[1, {x, -1, 1}, {y, -1, 1}, Mesh -> False, 
   PlotStyle -> Opacity[0.3]];
curves[angle_] := 
  ParametricPlot3D[{RotationMatrix[angle, {1, 0, 0}].{u , 0, 
       u^4 - 2} + {0, 0, 2}, {u, 0, 2}}, {u, -1, 1}, 
   PlotStyle -> {{Red, Thickness[0.02]}}];
Manipulate[Show[pp, plane, curves[a]], {a, 0, 2 Pi}]

Region rotated about the line y=2

3 Answers3

Edit

Linked