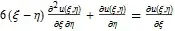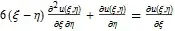The issue behind isn't simplification or output formating, but the ambiguous transformation rule and equation solving in complex domain. If you read the source code of DChange, you'll notice that it internally uses Solve to find the relationship between old variables and new variables like this:
……
variablesReplacements = Solve[transformations, oldVars][[1]]
……
it assumes there's only one representation for the old variables with new variables, which is certainly reasonable, but from your transformation rule, one can find 2 different representations for the old variables:
sol = Solve[{ξ == (3 y)/2 + Sqrt[-x]^3, η == (3 y)/2 - Sqrt[-x]^3}, {x, y}]
(* {{x -> -(-(1/2))^(2/3) (η - ξ)^(2/3), y -> (η + ξ)/3},
{x -> ((-1)^(1/3) (η - ξ)^(2/3))/2^(2/3), y -> (η + ξ)/3}} *)
Then DChange will select the first solution, which is actually not what you want:
sol[[1]] /. {η -> -1, ξ -> 1} // N
(* {x -> 0.5 + 0.866025 I, y -> 0.} *)
Use a unambiguous transformation will resolve the problem. If you want to simplify the result further with Assuming, Assuming only has effect on functions that accept Assumptions option, and the only function meets the requirement inside DChange is the Simplify in the last step, so you need to provide assumptions for η and ξ rather than x:
Assuming[η - ξ < 0,
pdConv[Column[DChange[{D[u[x, y], {x, 2}] + x*D[u[x, y], {y, 2}] == 0},
{(ξ - 3 y/2)^(1/3) == Sqrt[-x], (-η + 3 y/2)^(1/3) ==
Sqrt[-x]}, {x, y}, {ξ, η}, {u[x, y]}]]]]