0

For example I have PDE:

$\tan^2 x\frac{\partial^2 u}{\partial x^2}-2y \tan x \frac{\partial^2 u}{\partial x \partial y}+y^2\frac{\partial^2 u}{\partial y^2}+\tan^3 x \frac{\partial u}{\partial x}=0$

And I need to classify that PDE.

I don't know naming conventions for such subject and I will use this document (it mostly corresponds with my course of Mathematical physics): Second-Order linear PDE

I need to clarify that I need to demonstrate following steps: finding the discriminant, partial derivatives, and the resulting canonical form of the equation.

  1. $∆(L)(x,y)=(y\tan x)^2-(\tan^2x) y^2=0 \Rightarrow parabolic \; type$;
  2. Method of characteristics

$\tan^2 x(\mathrm{d}y)^2+2y\tan x \mathrm{d}x\mathrm{d}y+y^2(\mathrm{d}x)^2=0 \\ \tan x \mathrm{d}y+y\mathrm{d}x=0 \\ \tan x y'+y=0$

DSolve[Tan[x]*y'[x] + y[x] == 0, y[x], x] // Simplify;
res[x_] = y[x] /. %[[1]];
Solve[res[x] == y /. C[1] -> c, c][[1, 1]]

$c\to y \sin (x)$

  1. New variables:

$\left\{\begin{matrix} \xi & = & y\sin x & \\ \eta & = & x & \end{matrix}\right. $

  1. Finding partial derivatives and canonical form.

Code:

pdConv[f_] := TraditionalForm[f /. Derivative[inds__][g_][vars__] :>
 Apply[Defer[D[g[vars], ##]] &, 
  Transpose[{{vars}, {inds}}] /. {{var_, 0} :> 
   Sequence[], {var_, 1} :> {var}}]]
a[x_, y_] := (Tan[x])^2;
b[x_, y_] := -2 y*Tan[x];
c[x_, y_] := y^2;
d[x_, y_] := ((Tan[x])^3)*D[u[x, y], {x, 1}];
res = DChange[
  {
   D[u[x, y], {x, 1}],
   D[u[x, y], {y, 1}],
   D[u[x, y], {x, 2}],
   D[u[x, y], {y, 2}],
   D[u[x, y], x, y],
   a[x, y]*D[u[x, y], {x, 2}] + b[x, y]*D[u[x, y], x, y] + 
     c[x, y]*D[u[x, y], {y, 2}] + d[x, y] == 0
   },
  {ξ == y*Sin[x], η == x},
  {x, y},
  {ξ, η},
  {u[x, y]}
] 
formatted = pdConv[res]

Next part of code you can see on the screenshot (I defeated insert it as code):

code

  • Can I get result such as in the last part (after ToString) and don't lose style after pdConv?

  • Is it badly to get error with Solve? All right or an error occurred?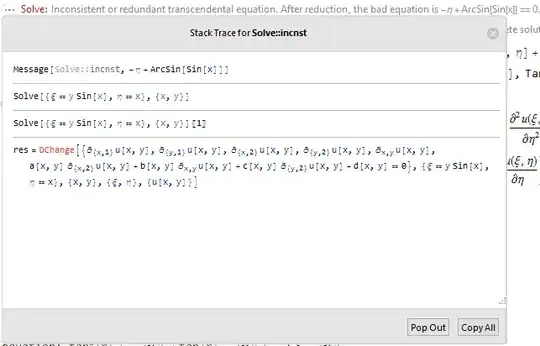 error

P.S. pdConv from here, DChange from answer.

P.P.S. Please do not judge strictly. I am a newbie. Any tips are welcome.

Community
  • 1
Woland
  • 215
  • 1
  • 5
  • What do you mean by "Can I get result such as in the last part (after ToString) and don't lose style after pdConv?" As to the 2nd question, the underlying issue is the same as that of your previous question: your transformation rule is ambiguous. The warning will disappear if you use ArcSin[\[Xi]/y] == x instead, but in this case it's not necessary because Solve still manage to find the correct result. – xzczd Oct 23 '16 at 04:04
  • @xzczd Please, check the screenshot. Compare style of Out[98] and Out[99]. I want to add labels for derivatives. Because it is difficult to navigate in the result set. So I convert result with help of the ToString and add text. But ToString breaks style as you can see. I didn't thought up any better way; Can you help me avoid ambiguous transformation rules? Are there some tips? – Woland Oct 23 '16 at 08:35
  • You mean the style of %99 is no longer the same as %98? Then wrap another TraditionalForm outside of the string i.e. TraditionalForm[(*first string*) <> ToString[formatted[[1, 1]], TraditionalForm]]. As to the second question, just consider if your equations can deduce a unique rule. If you're not sure, try solving out the new variables and old variables from the equation respectively with Solve first and see if Solve complains or gives multiple solutions, if not, then the transformation rule is OK, never forget DChange is built on Solve. – xzczd Oct 23 '16 at 08:58
  • @xzczd OK, ty. Can you help me with assuming for x and y? Now I know from previous question, that Assuming before DChange is for ξ and η. But what if I have no idea how convert limitations for x and y to limitations for ξ and η? I have tried insert Assuming into DChange params but no result... For example x>0 && y<0. Where can I tell Mathematica about that? – Woland Oct 23 '16 at 16:33
  • As mentioned in the previous answer, Assuming only has effect on functions with an Assumption option, while Solve doesn't have one. It currently only accepts assumptions in this form: Solve[{\[Xi] == y*Sin[x], \[Eta] == x, -Pi/2 <= x <= Pi/2}, {x, y}]. Of course it's not hard to modify the code of DChange to make it accept assumption. You may also suggest adding an e.g. solveAssumption option to the author of DChange. – xzczd Oct 24 '16 at 01:18

0 Answers0